ML_2021_1-1 監督式學習概論

發表於 更新於

前言：什麼是機器學習

機器學習，就是用機器的力量幫忙找出一個合適的函數

  • 函數的輸入可以是vector、matrix、sequence
  • 輸出可以是數值(regression)、類別(classification)、文章、圖片
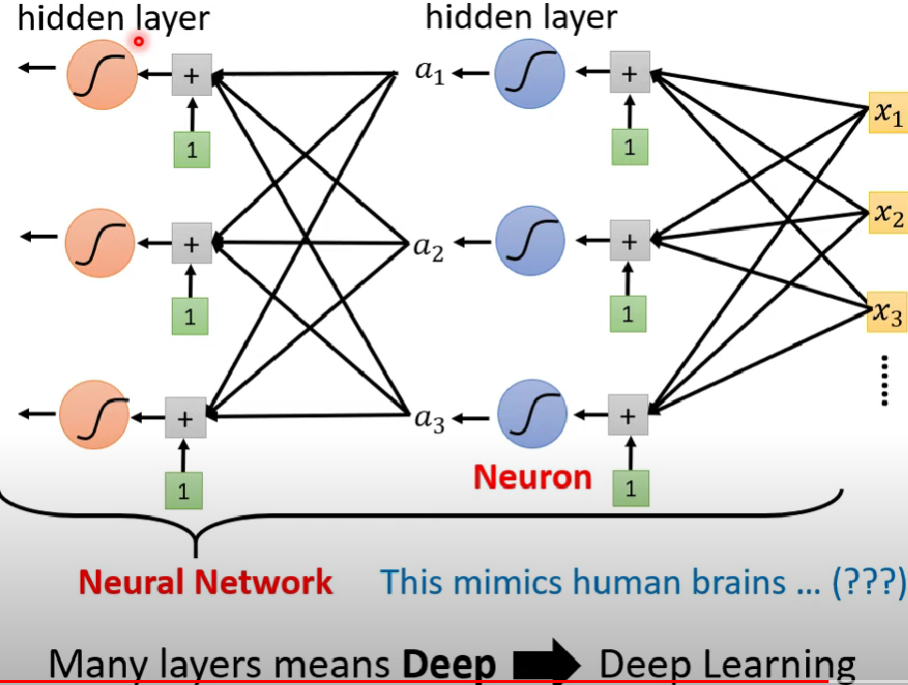
    深度學習，就是用神經網路的方法來製造函數

預測頻道觀看人數

基本原理

  • loss function的輸入是weight跟bias，輸出是這組參數有多好」
  • Optimization : 找出最好的一組參數(w*,b*)使loss function最小
    • 常用gradient descent
      • 隨機決定w_0
      • 把L對w做偏微分，若斜率>0則提高w，反之降低w(變動量=η，屬於hyperparameters)
step1: 製作一個學習函數

純粹Linear Model

  1. 先隨便設一個函數
    $$f = w_0 x_1$$
    其中$x_1$是昨天的觀看人數

  2. 根據loss function的結果嘗試把$w$、$b$優化，使得$f = w_0 x_1 + b$有最小損失函數(這裡優化方法採梯度下降)

  3. 跑測試結果發現$w$很接近1 (看似很合理，因為昨天的頻道觀看人數與今天的頻道觀看人數差距應該不多)，其實預測都是前一天的結果平移而已，命中率有限 -> 試試看一次看多幾天，變成以周為單位

  4. 修改函數
    $$f_1 \leftarrow y = b+ \sum_{j=1}^7 w_j x_j$$
    表示預測一天的觀看人數，需要前面七天觀看人數作為參考

  5. 命中率有效提高了（這是linear model）

Piecewise Linear Curve

  • linear model過於簡單，x與y之間的關係是直線(w改動斜率，b改動原點)
  • 利用一系列的線性函數相加，使加總後的函數有彎折
  • Piecewise Linear Curve = constant + sum of a set of 藍線 (下圖紅線就是我們想求的「預測模型」函數f )
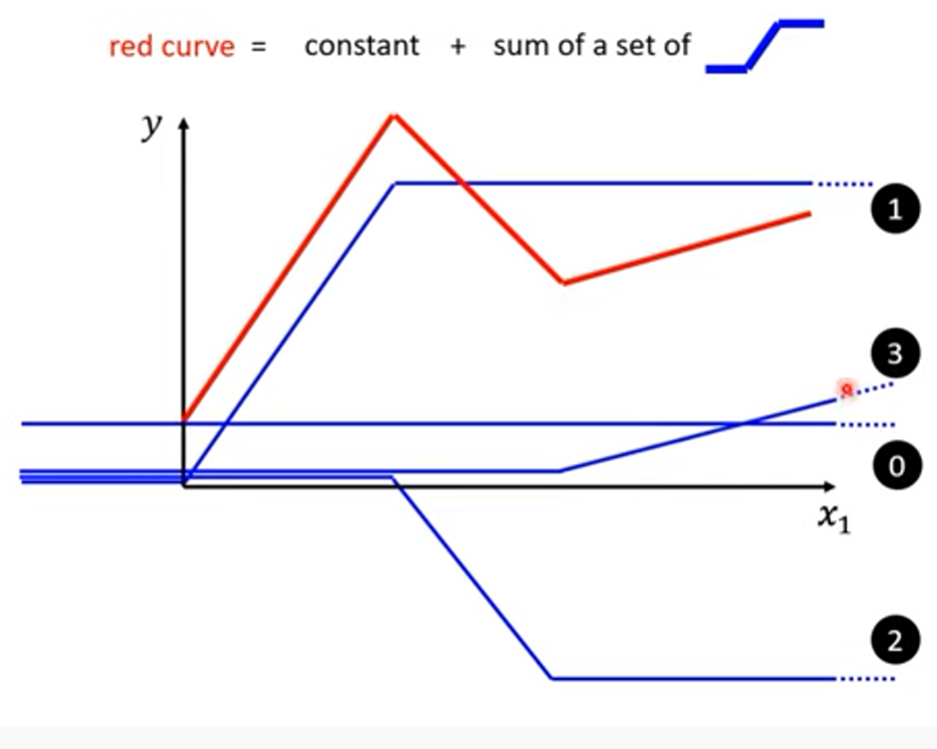
  • 假設有無窮多個藍色function，就可以塑造出任意形狀的紅色function，如上圖所示

當特徵=1

  • 如何寫出藍線式子?
    • 藍線函數令為 $f_{blue1} \leftarrow y = c_i sigmoid(b_i+w_ix_1)$
    • 使用sigmoid，把藍線變成曲型來逼近原型
    • 原型稱為hard sigmoid
    • 讓藍線凸在對的地方->修改w,b,c
  • 綜合前面的內容，我們就可以求得單一feature下的紅色function(而這樣理論上可以逼近任何連續函數)：
    $$f_{red1} \leftarrow y = b + \sum_{i}c_i sigmoid(b_i + w_ix_1)$$
  • 其中b也可以根據不同藍色function有所不同，把b丟入$\sum$即可

當特徵>1

  • 當然，我們也可以進一步推廣，增加feature的量(目前只有一個，$x_1$的某特徵乘上各藍線的$w_i$)

  • 解法就是修改藍線函數變成$f_{blue2} \leftarrow y = c_i sigmoid(b_i + \sum_{j} w_{ij}x_j)$
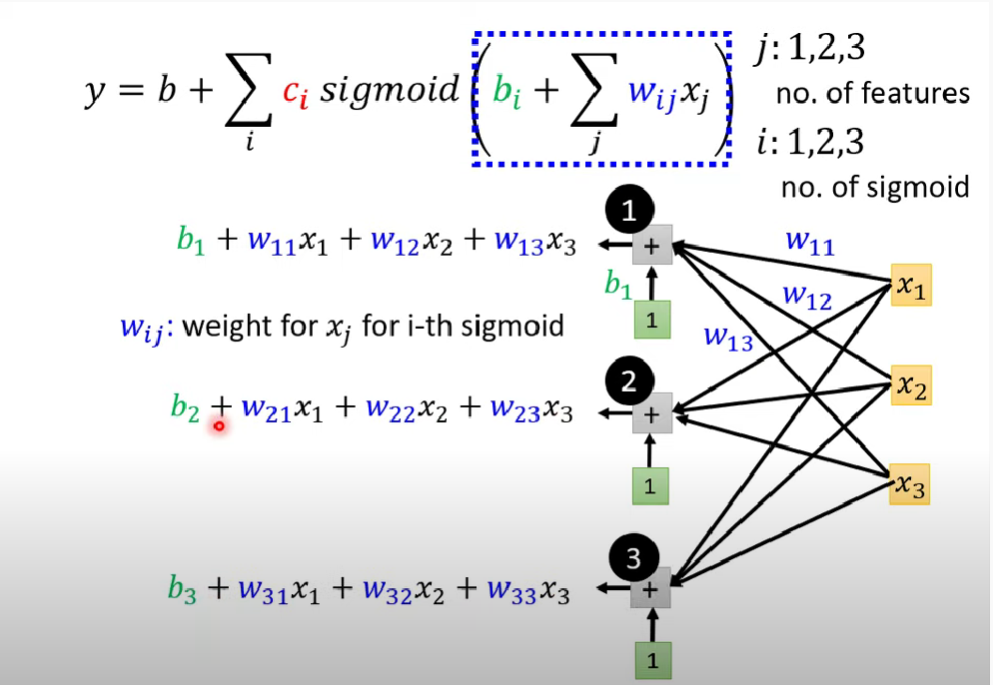
    upload successful

  • 同理把藍色函數相加再補上常數，紅線函數則可令為
    $$f_{red2} \leftarrow y = b + \sum_{i}c_i sigmoid(b_i + \sum_jw_{ij}x_j) $$

  • $w_{ij}$表示第i個sigmoid函數(aka第i條藍線)中，對於第$x_j$個特徵的權重

    用線性代數的方式來理解
    • 繼續剛剛特徵>1的討論
    • 令$r_i = b_i + \sum_{j}w_{ij}x_j$ (換句話說r就是sigmoid函數內的運算結果)，則可以把這個等式簡化為一個矩陣相乘
      函數的示意圖如下:
      upload successful
    • 而$r_i$做sigmoid()以後就會得到$a_i$
    • 又稱$a = \sigma(r)$
    • 最後把$a_i$乘上各自的$c_i$後，加總得到剛剛的$f_{red2}$ (c在相乘時是$c^T$矩陣)
    • $b、c^T、b_i、W、x$五個向量append起來以後統稱為$\theta$

    upload successful

step2: 定義訓練資料的損失函數
  • Loss is a function of parameters $L(\theta)$ ($\theta$就是step1中的那個)
  • 就是x丟進去，測量y-hat跟y的差別多大
step3: 最佳化模型
  • 假設最佳化的參數向量是$\theta^*$
  • 則$\theta^* = arg$ $min_{\theta}L$
  • 首先，隨機選一個$\theta^0$作為初始值
  • Gradient descent作法
    $$
    g^T =
    \begin{bmatrix}
    \frac{\partial L}{\partial \theta_1}\
    \frac{\partial L}{\partial \theta_2}\
    \frac{\partial L}{\partial \theta_3}\
    \ldots
    \end{bmatrix} |_{\theta = \theta_0}
    $$
    • 註：打不出1xn向量= =
  • 則稱 g = $\nabla L(\theta^0)$

 求出g向量以後，就可以把它拿來更新參數列:
 

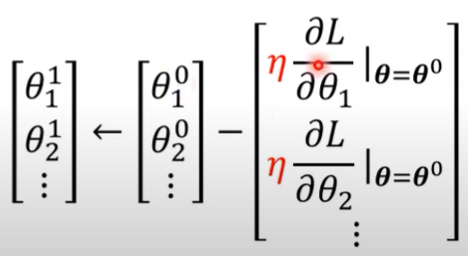
  • 亦即 $ \theta_1 \leftarrow \theta_0 - \eta g $

Note

  1. 實務上通常做gradient不是所有資料都加入去更新，而是先把資料切成batch分別計算出$L^i$

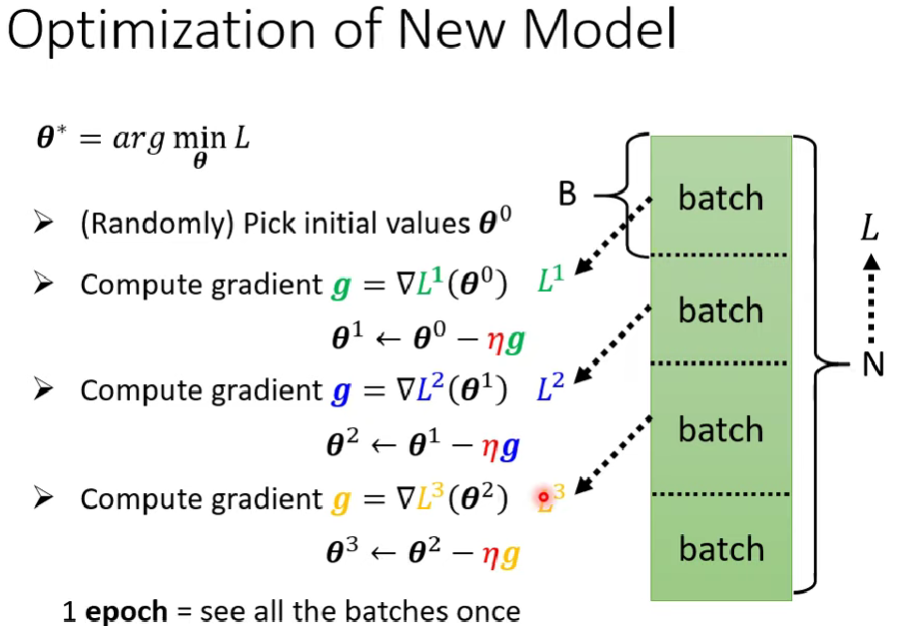
upload successful

  • 一次的更新$\theta$是一次update，一次看完所有batch算一次epoch
    • 所以一個epoch會有好幾次update
  1. Hard sigmoid也可以用兩個ReLU做出來

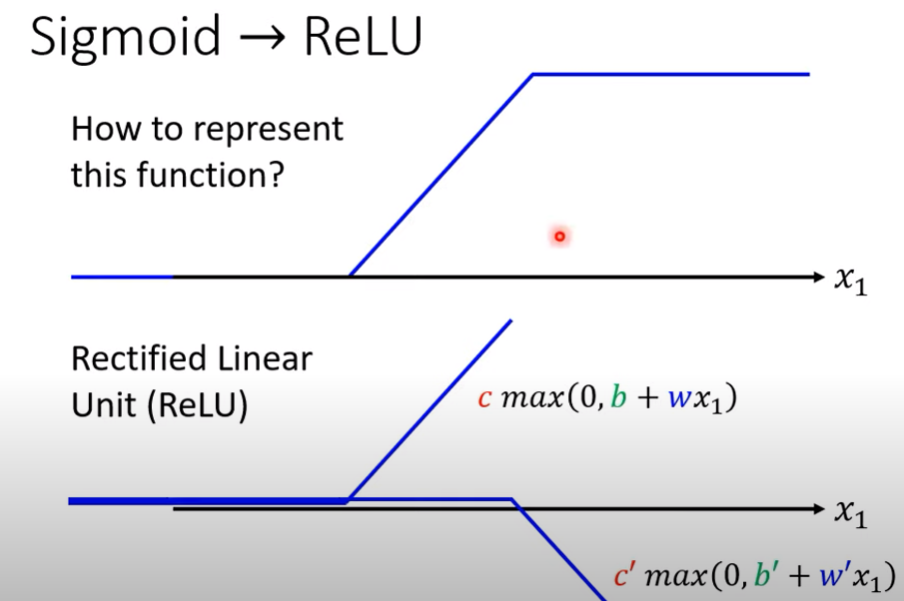
upload successful

  • 當然因為是要用兩個ReLU做出來，所以相應的紅線函數就要改
    $$
    f_{red_{ReLU}} \leftarrow y = \sum_{i}c_i max(0,b_i + \sum_j w_{ij}x_j)
    $$
  • 這種做法比sigmoid好(下周講解)
  • ReLU跟sigmoid同為activation function

 

step4: 繼續修改模型 

 - 同樣的求a過程，我們可以做好幾次

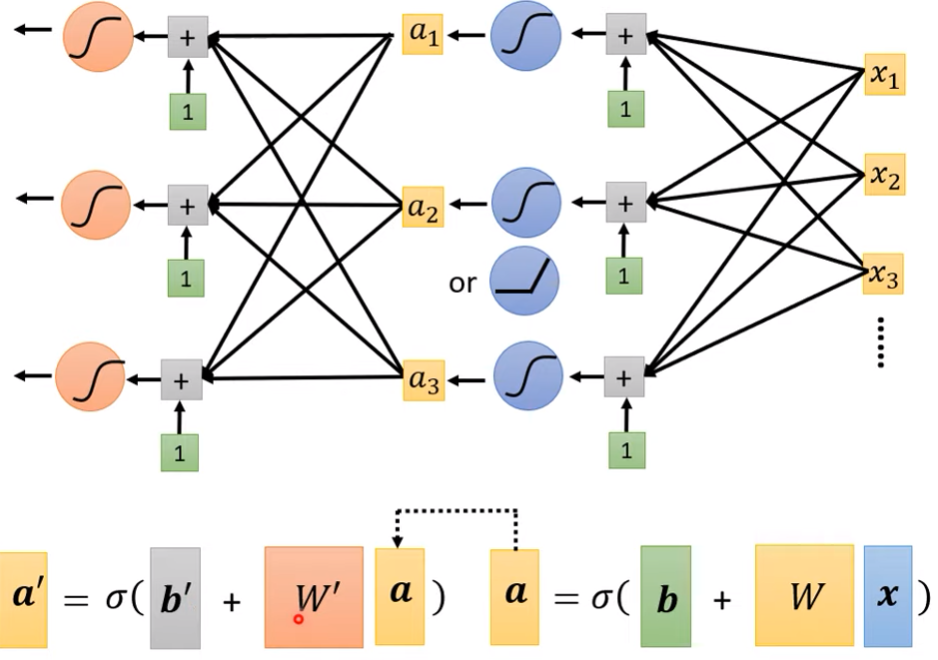
upload successful
   注意，圖中的W’、W、b’、b互不相同

 - 要做幾層同屬hyper parameter
 


 名詞解釋
 
upload successful