ML_2021_2-2 類神經網路訓練不起來怎麼辦(一)
這裡只討論optimazion失靈的時候,如何把梯度下降做得更好
為何opti會失敗(grad)?
- gradient decent=0,使參數無法再更新
- 點卡在local minima or saddle point(稱為卡在critical point)
分辨critical point是saddle point or local minima
- 雖然我們無法知道loss function長怎樣,但可以用泰勒展開式逼近
- 給定一組參數$\theta’$
- 則使用tayler series approximation
原式為
$$
f(x) = f(a) + \frac{f’(a)}{1!}(x-a) + \frac{f’’(a)}{2!}(x-a)^2 + ….
$$
我們取到2次微分,代入$x = \theta及a = \theta’$得到
$$
L(\theta) \sim L(\theta’)^Tg + \frac{1}{2}(\theta - \theta’)^TH(\theta - \theta’)
,其中 g = \nabla L(\theta’)(請參考上週)
$$

其實g就是$L(\theta’)$對$\theta_i$的一階微分,Hessian是$L(\theta’)$對$\theta_{ij}$做二次微分
因為critical point的時候g = 0,所以我們要考慮H(也就是2次微分的部分)來分辨是哪種問題,2次微分可以看出地貌
把Hessian部分拉出來討論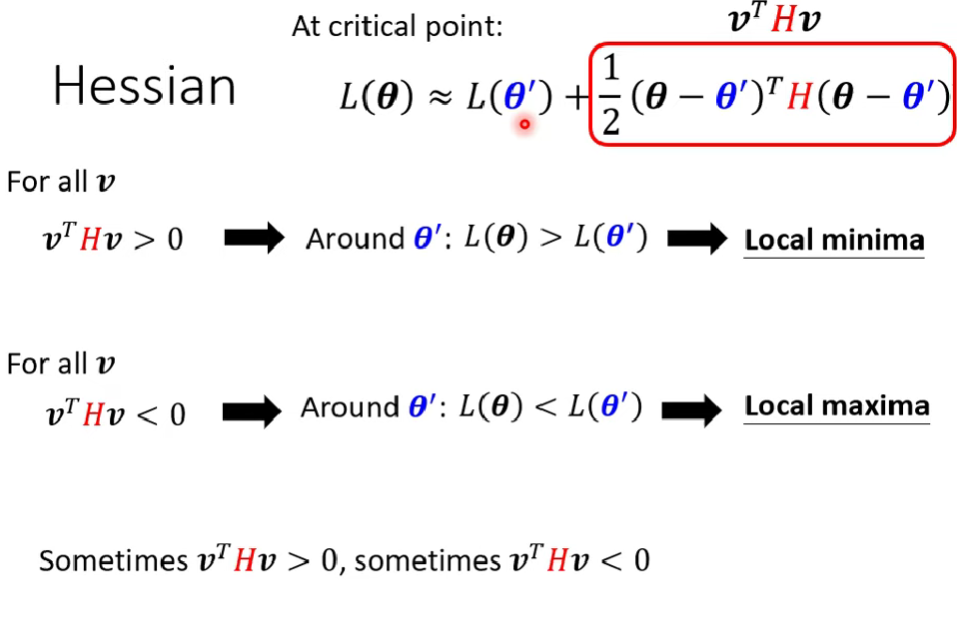
要如何確認滿足哪個原因呢?- 線性代數:正定、負定、均非 (看H的eigen value)
範例說明
給定一個模型$y = w_1w_2x$,資料僅有一筆,$f(1)$時其label = 1,且w1w2之間不具有任何激發函數,loss function採用MSE
則x=1時透過爆搜我們可以得出下面的error surface(偷偷看正解圖)
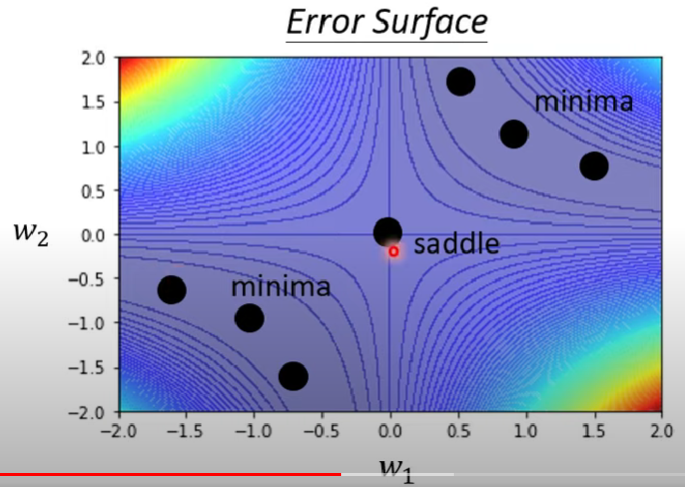
其中鞍點的四周都是高牆,無法離開
局部最小點則是在範圍內找不到更低的點
但假設我們不知道這個error surface,我們可以應用上面的方法來測定他是哪個問題,根據MSE公式我們得出
$$
L = (\hat{y}-w_1w_2x)^2 = (1-w_1w_2)^2
$$
對他們做微分可以得到(注意chain rule)
$$
g = \frac{\partial L}{\partial w_1} = 2(1-w_1w_2)(-w_2)
$$
$$
g = \frac{\partial L}{\partial w_2} = 2(1-w_1w_2)(-w_1)
$$
代入g=0,可以發現當$w_1 = w_2 = 0$,有critical point
接下來要確認他們是哪個問題,就繼續再做微分: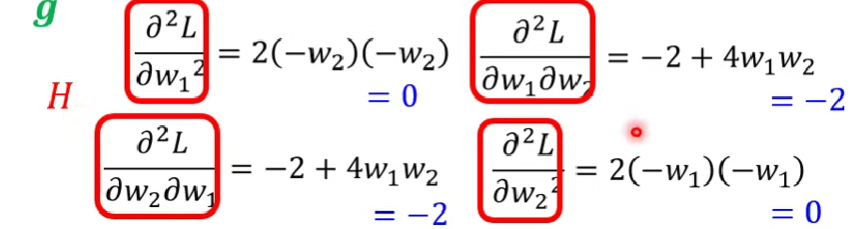
代入剛剛的$w_1 = w_2 = 0$得到
$$
H =
\left[
\begin{matrix}
0 && -2 \\\ -2 && 0
\end{matrix}
\right] \tag{3}
$$
抓H的eigen values來知道他是哪個point
case: saddle point
- 我們可以藉由H來得到參數該移動的方向
令$\lambda$是H的一個eigen value, u為$\lambda$的其中一個eigen vector
則
$$
v^THv = u^THu = u^T(\lambda u) = \lambda \vert \vert u \vert \vert^2
$$
若今天$\lambda < 0$則必定$u^THu<0$,回顧剛剛的式子
$$
L(\theta) \sim L(\theta’)^Tg + \frac{1}{2}(\theta - \theta’)^TH(\theta - \theta’)
$$
可以知道$L(\theta)必定>L(\theta’)$
我們只要將$\theta’沿著u的方向更新u得到\theta$,就可以再次降低loss
範例說明
- 延續剛剛的例子,我們知道$H的\lambda_1 = 2, \lambda_2 =-2$,屬於saddle point(非正定與負定)
- 取$\lambda_2 = -2 , u = (1,1)$,則把$\theta = (0,0)+(1,1)$,就可以逃出saddle point
- 實務上不易使用,因為要做出2次微分且還需要用到找出該矩陣的eigen value,計算量過大 (還有別招可以用)
Saddle point vs. Local Minima
- 在三維的密閉石棺中,在更高維度未必是密閉的
- 在低維度的local minima中,是否只是高維中的saddle point?
- 當參數超級多,是否極度有可能local minima其實只是saddle point? (假說)
- 在實作中,絕大多數的模型,critical point所在點中,幾乎找不到所有eigen value均>0的範例,表示我們幾乎不可能找到完全的local minima
- 定義一個數值”Minimum ratio = $\frac{正\lambda數}{\lambda數}$”,表示你的critical point有多像local minima
- 所以我們可以知道,通常一個模型train到loss卡住,極高可能是卡在一個saddle point