ML_2021_2-4 類神經網路訓練不起來怎麼辦(三)

發表於 更新於
  • Critical point 不一定是在訓練模型時會碰到的最大問題

Adaptive Learning Rate

  • 我們都認為training loss卡住了之後，是因為parameters卡在critical point
  • 其實有可能是loss function在兩個谷間碰撞，可能是兩組parameters之間剛好loss差不多
  • 考慮一個情境，高爾夫球一直在球洞兩邊滾來滾去，就是滾不到終點
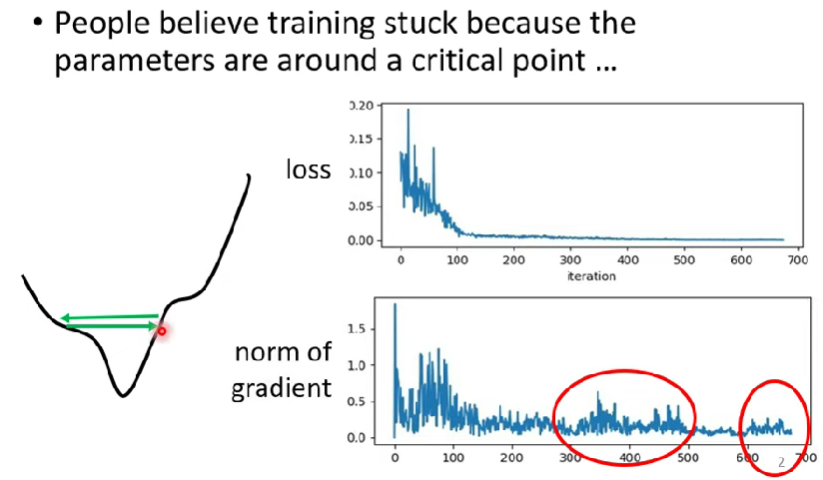
  • 多數training其實還沒走到critical point就已經停止 (所以真正要注意的點不是critical point)

非卡在critical point的Example

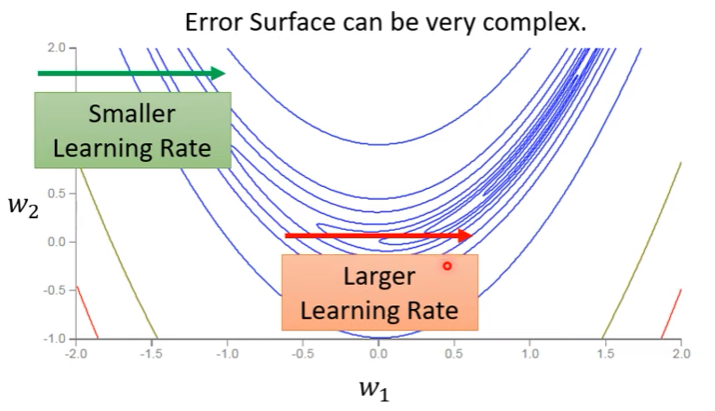
  • 給定一個convex error surface，如下圖
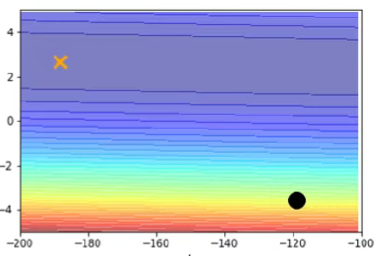
    upload successful

  • 當learning rate太大，會容易在等高線密集的地方邁步過大，如下圖
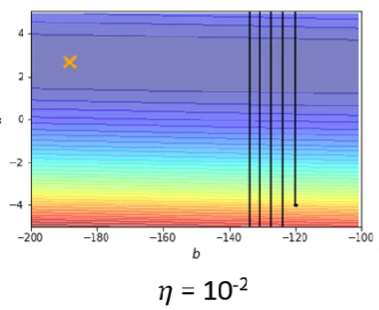
    upload successful

  • 或是當learning rate太小，容易卡在低谷幾乎動不了(要挪到X需要好幾百萬次更新)，如下圖
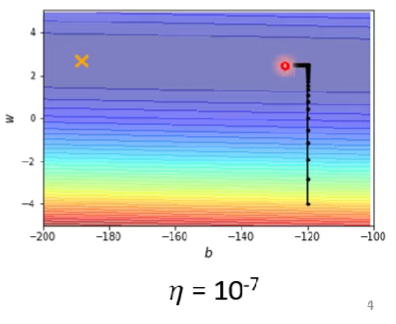
    upload successful

$\rightarrow$ 單一learning rate通常不能貫徹模型訓練的整個過程

如何設定learning rate? - Adagrad Approach

  • 從上個例子可知，當某方向上等高線密集時，我們需要learning rate 小，反之則要大

  • 為了讓$\eta$能自動變動，要調整公式

  • 下圖為梯度下降法的原始公式
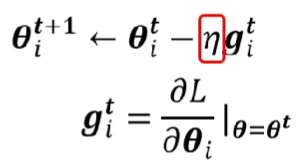
    upload successful

  • 方便起見，這裡只用一個參數

  • 更動以後的算式如下

$$
\theta^{t+1}_i \leftarrow \theta^t_i - \frac{\eta}{\sigma^t_i} g^t_i
$$

  • 我們讓$\sigma^t_i$加入等式，這樣就可以讓learning rate變成一個parameter dependent的hyper parameter

如何計算sigma?

$$
\theta^{1}_i \leftarrow \theta^0_i - \frac{\eta}{\sigma^0_i} g^0_i
$$
其中$\sigma^0_i = \sqrt{(g^0_i)^2} = \vert g^0_i \vert$
接下來
$$
\theta^{2}_i \leftarrow \theta^1_i - \frac{\eta}{\sigma^0_i} g^1_i
$$
其中$\sigma^1_i = \sqrt{\frac{1}{2}[(g^0_i)^2+(g^1_i)^2]}$

…
一路推廣，可以得到

$$
\theta^{t+1}_i \leftarrow \theta^t_i - \frac{\eta}{\sigma^t_i} g^t_i
$$

其中

$$
\sigma^t_i = \sqrt{\frac{1}{t+1}\sum_{j=0}^{t}(g_i^j)^2}
$$

  • 目前這個技巧應用在Adagrad

原理

  • 當gradient小(平坦)，算出來的$\sigma$就小，learning rate大
  • 當gradient大(陡峭)，算出來的$\sigma$就大，learning rate小

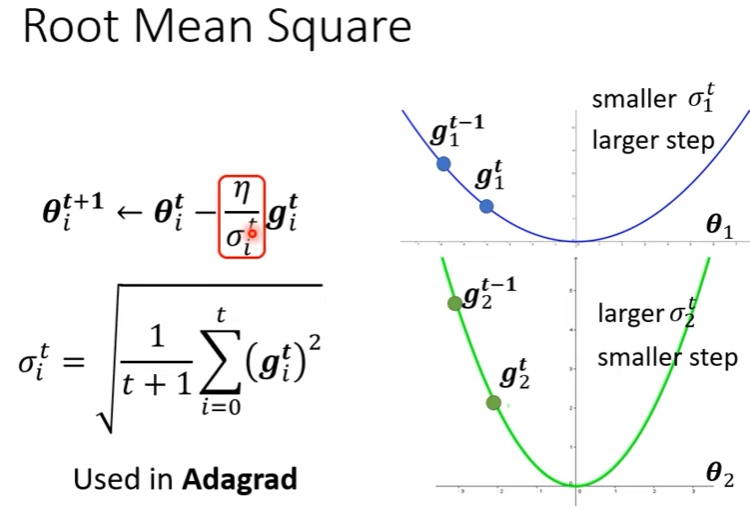
這樣會有甚麼問題

  • 剛才的假設是同一個參數，他的gradient大小就固定一個值(?)
  • 就算是同一個參數，他需要的learning rate也會隨時間而改變
  • 我們期待就算是同一個參數在同一個方向，learning rate也會有所改變
    舉例，我們討論橫軸

upload successful

如何設定learning rate? - RMSProp Approach

  • 一個沒有論文的方法orz
  • 方法如下圖
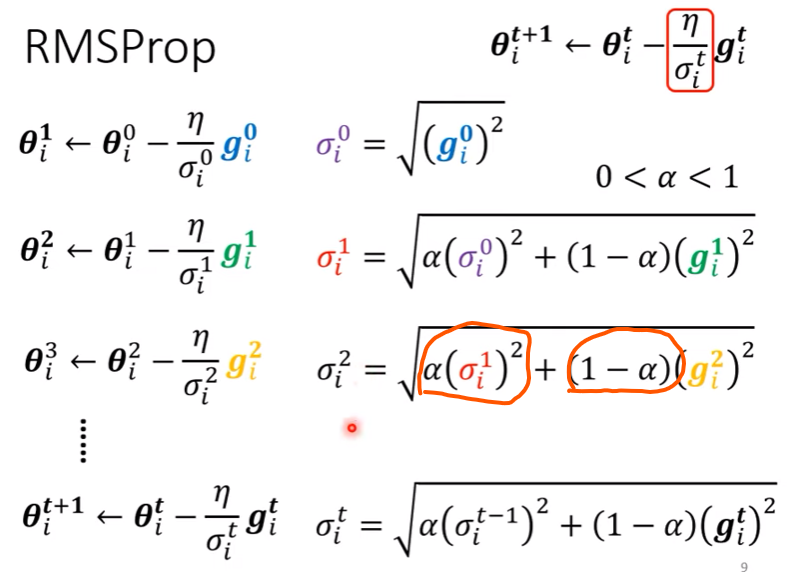
  • 主要改變了紅圈圈起來的部分，捨棄了用前面所有的gradient求MSE決定$\sigma$的方法，RMSProp只採計上一個$\sigma$值以及這次的gradient之MSE和
  • 多了一個hyper parameter $alpha$，調整對上一個$\sigma$的學習率高低
  • 其實上一個$\sigma$就包含了前面所有的gradient之MSE，只是權重會隨著疊代越來越小

learning rate變動範例圖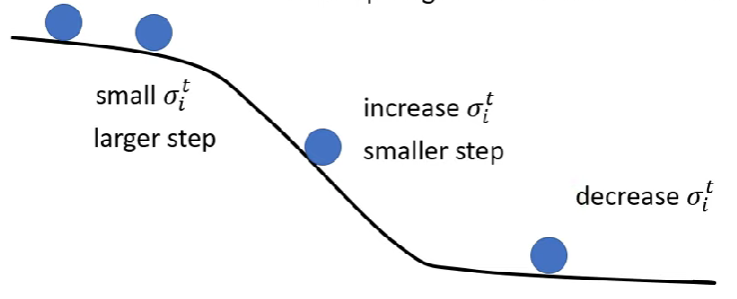

回到一開始的範例

  • [回到這個範例](# 非卡在critical point的Example)，我們來看看各approach的效果

Adaptive learning rate

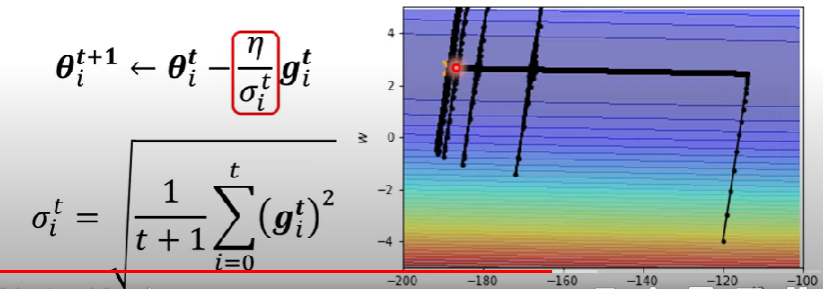
filename already exists, renamed

  • 為啥爆炸了?
    • 根據公式，我們把前面幾次的gradient都列入計算，因為在橫線的部分步伐很大，所以當走到步伐該縮小的時候，會爆衝
         - 但也因為公式，爆衝一陣子以後learning rate會逐漸縮小，然後回歸正軌，等待一陣子以後learning rate上升再度爆炸
解法：learning rate decay
  • 隨著訓練的進行，我們一定越來越接近終點
  • 可以隨著時間降低learning rate，開始微調
解法2：Warm up

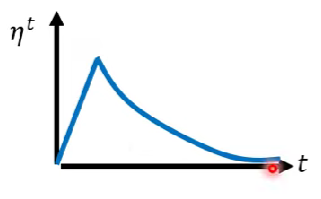
  • 算是一種黑科技
  • 先變大learning rate，再縮小(?)
  • 在訓練bert的時候常常用到，但他在很久以前就出現在論文過了
  • 在transformer中也出現過，見下圖
  • 一種可能的解釋是，因為$\sigma$是統計的數據，在訓練初期的時候容易失準，故初期讓learning rate小，等到$\sigma$精準一點以後，再讓learning rate變高
  • 相關paper : RAdam

Summary of Optimization

  • 雖然Momentum跟$\sigma$都使用過去的資料，但不會因此抵銷
    • Momentum是把所有gradient加起來，故有考慮方向與正負號
    • $\sigma$只考慮MSE

下次預告

  • 當訓練過程遭遇大山，要如何闢路繞過去？
  • 有沒有可能直接炸掉大山，改變error surface呢?
    $\rightarrow$ Batch normalization
    PS. 課程跳到2-6哦

Note

  • 現今最常見的Optimizer:Adam其實就是RMSProp + Momentum

  • Adam的細節自行參考

  • arxiv論文年代看法