ML_2021_4-1 自注意力機制（上）

發表於 更新於
  • 至今為止，我們network input 都是一個vector
  • 那如果輸入是可變動的一排向量（sequence）呢？

Vector set as input

  • 長度不一的句子就是一個範例
  • 關於word embedding如何得到，可以參考這個影片
  • 現在的文字基本上都是被word embedding過，而句子就是一連串了文字向量
  • 一段聲音訊號也是一個範例（25 millisecond），一個向量稱為『frame』
  • 一個graph也是一連串的向量
    • Drug discovery中一個分子，可以看做一個graph
    • 社群媒體中，人（節點）可以是一個向量，ex.性別、年齡、工作等等

What is the output?

Type 1 (本課專注)

  • 每一個vector都會有一個label
  • POS tagging（詞性標注），每一個詞彙都要對應一個詞性
  • 語音，每一段frame都會有一個Pheonic
  • Social network，對每一個人可能會有一種廣告投放方式

Type 2 (hw4)

  • 一整個sequence輸出一個label
  • Sentiment analysis: 機器去判讀一段句字是正面的還是負面
  • 給定一段音訊，分辨它是哪個人說的

Type 3

  • 不知道輸出幾個label
  • 稱為sequence to sequence(seq2seq)

Sequence labeling

  • 對於每個向量，要做一個label

First approach

  • 直接用fully connect network
  • 問題出現：同樣輸入就會有同樣輸出，但是不能保證兩個vector之間是否有關連
  • 需要consider the context

Second approach

  • 直接給fully connected network整個window (hw2就是這樣做的)
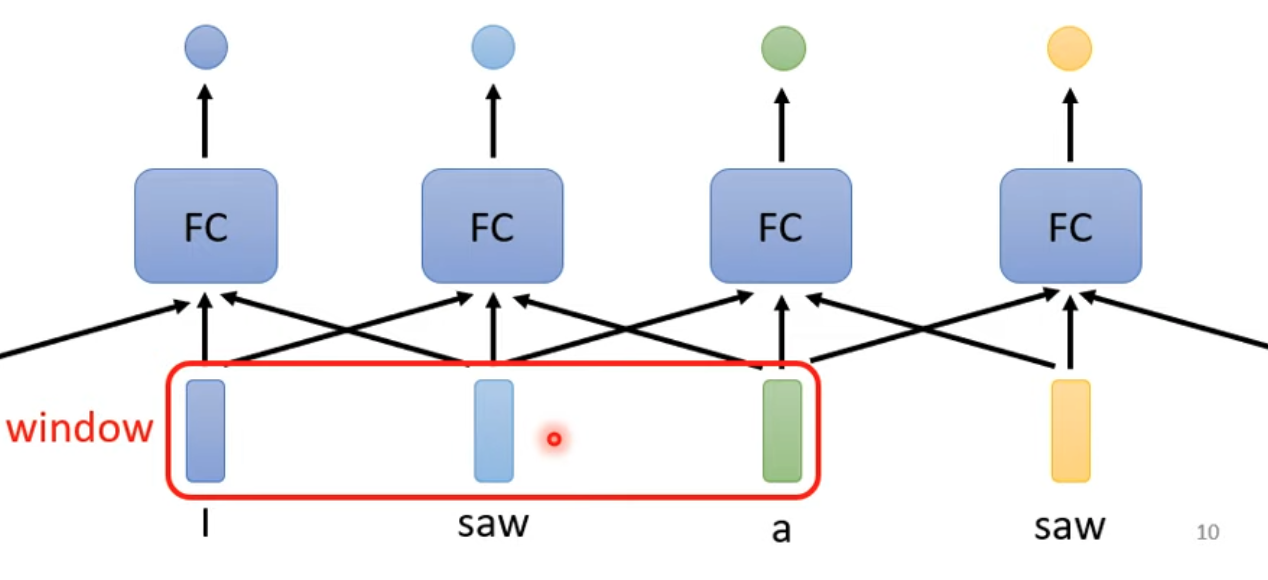
  • 問題：如果今天的任務是得要考慮整個sequence怎辦
    • sequence長度有長有短，window大小要變動，而且運算量非常大又導致overfitting

Third approach

  • 採用Self-attention技術，先把向量加工再個別丟入全連階層
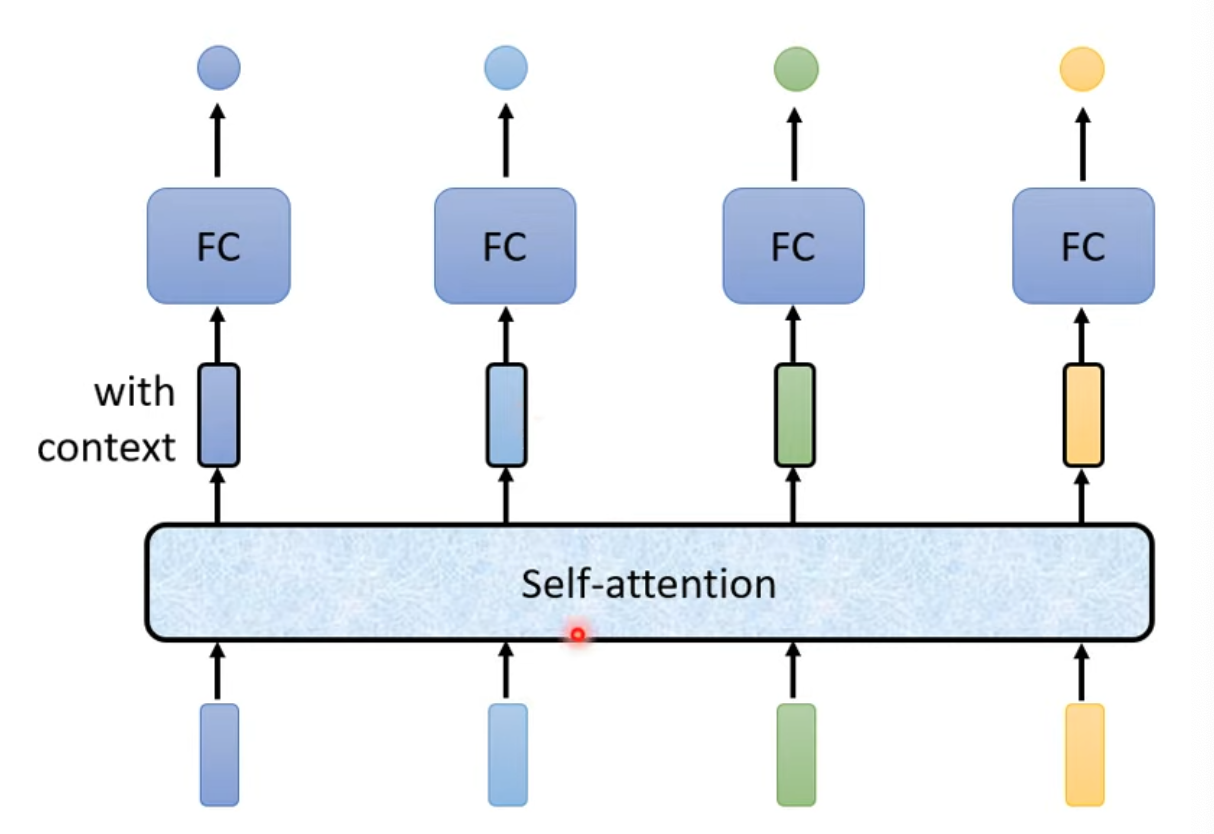
    upload successful
  • 黑框框向量表示考慮過前後文的加工向量
  • Self-attention可以有很多層
  • 經典論文：Attention is all you need
    • Transformer
  • Self-attention內部結構如下：
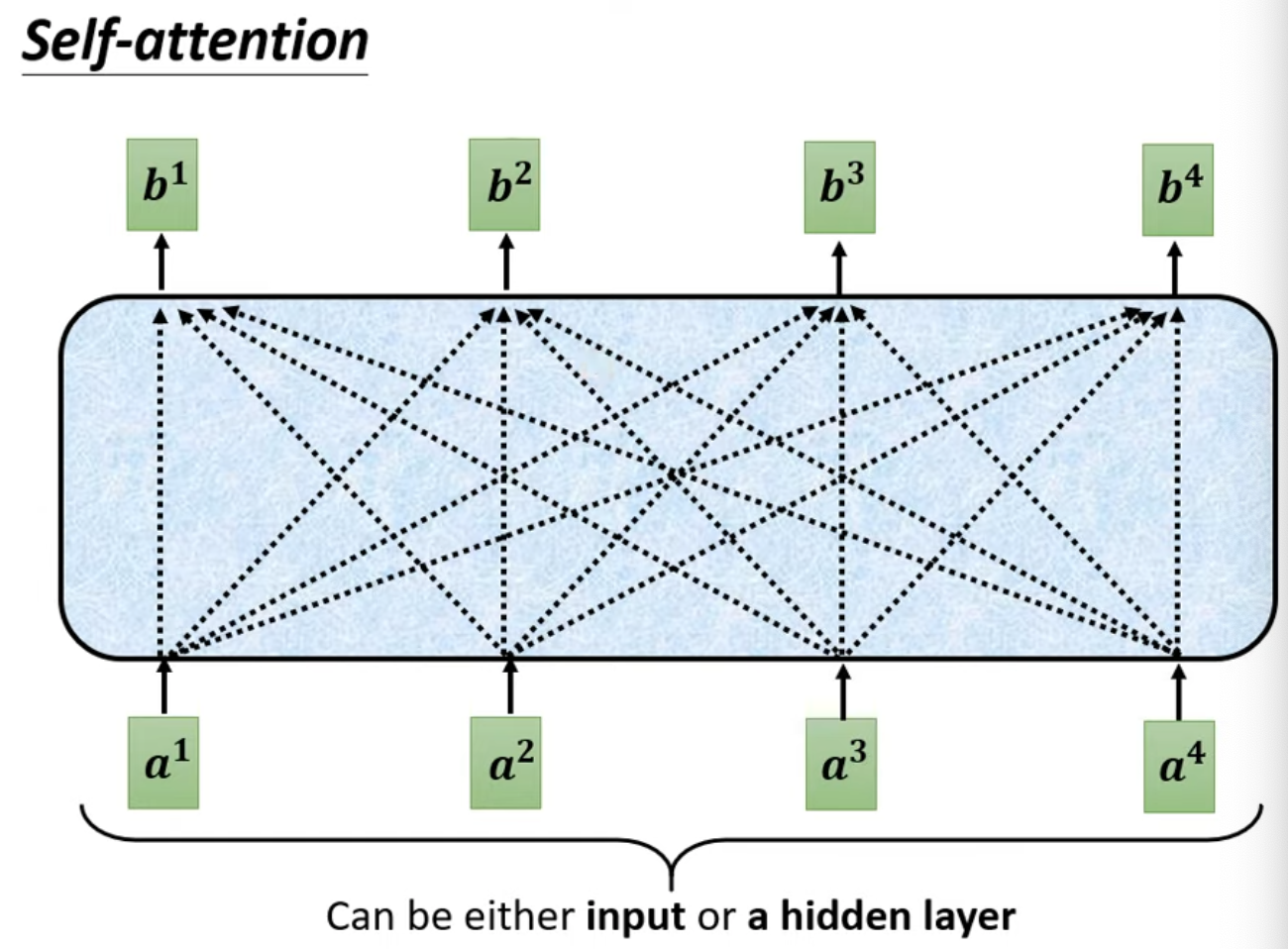
  • 找出relevant vectors in a sequence，關聯度以$\alpha$表示
  • 計算$\alpha$比較常見的做法是做內積，兩個向量各自乘一個矩陣($W^q、W^k等$)以後再做內積
    • 之後課程先只用這個方法

How to apply

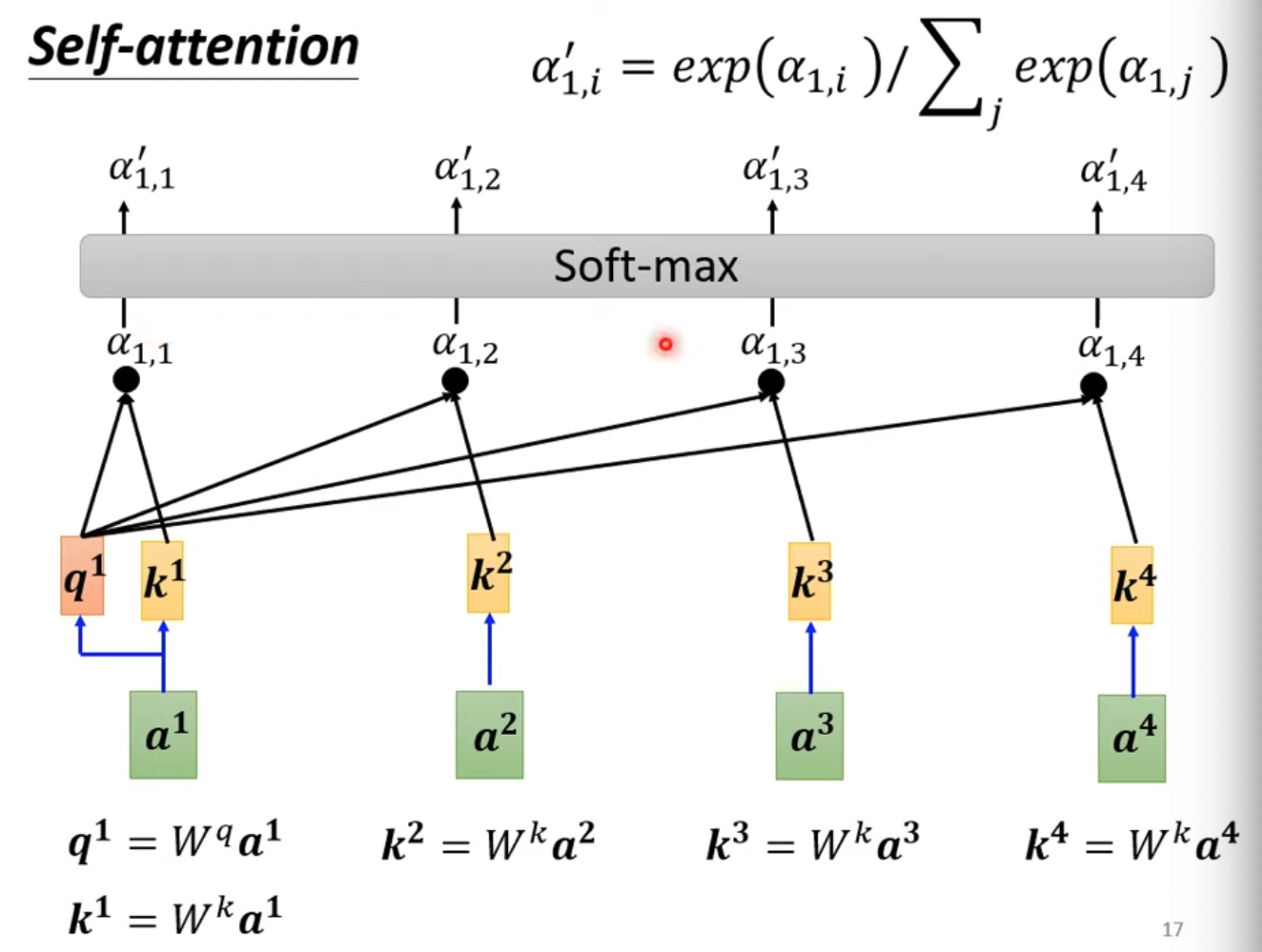
  • $q^1$表示輸入向量$a^1$對$W^q$矩陣相乘的結果
  • $k^i$則表示內積的另一個算子，表示$a^i * W^k$以後的結果
  • softmax不一定是唯一解，只是常見（用他沒有理由）
  • 得出$\alpha’$以後，繼續根據他抽取sequence中重要的資訊
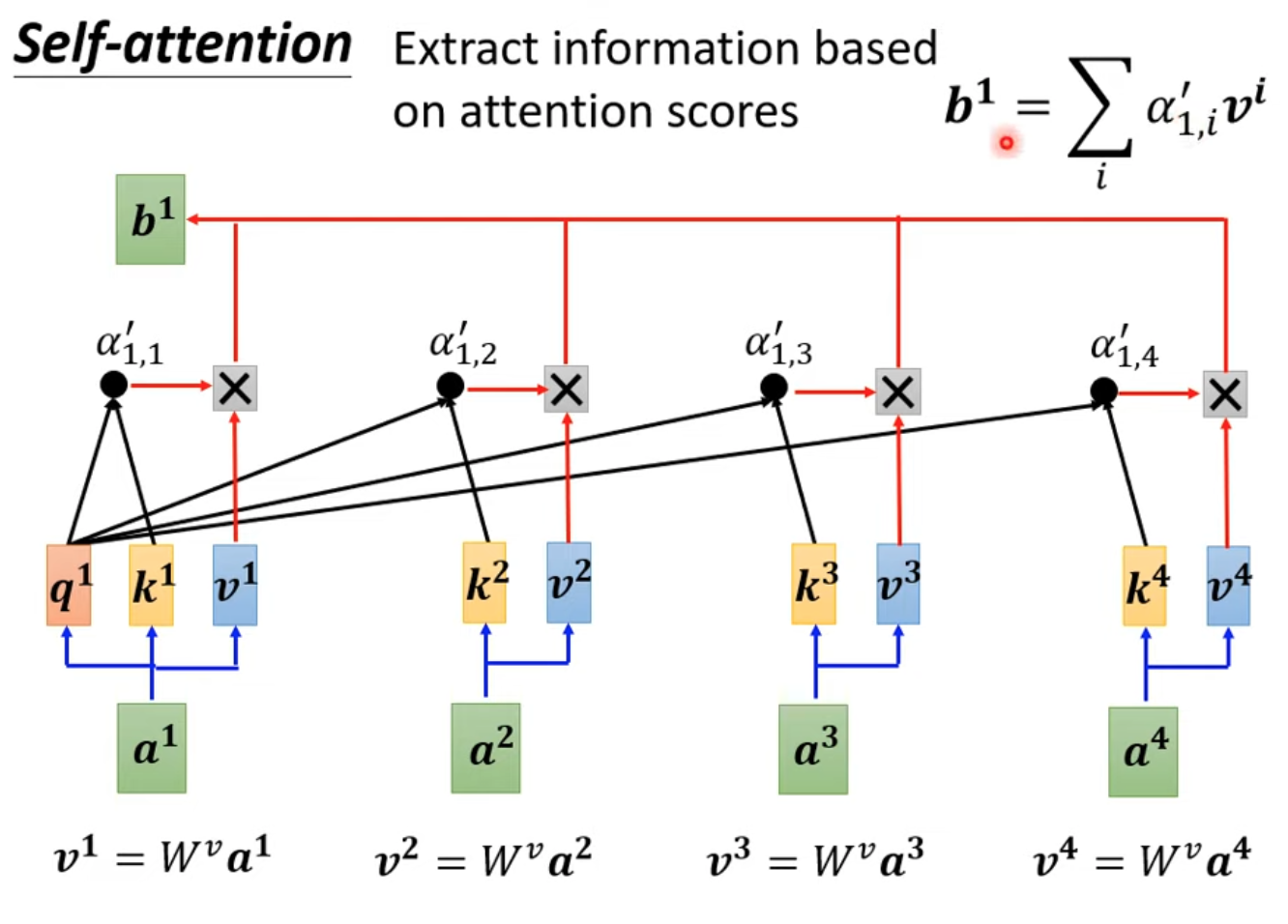
  • 最後再把$\alpha’$乘上$W^v$，一個向量得到的分數越高，則越可能會dominate抽取出的結果

參考文章

  • q:query，就是輸入的vector，用於與k做內積來判斷相似性
  • k:key，指序列中的所有詞向量
  • v:value，指實際的序列內容
  • q,k內積的過程稱為Dot-product Attention
  • 兩個vector之間的關聯越大，則 $\alpha$ 越大
  • 上面步驟講到的都是encoder