ML_2021_4-2 自注意力機制（下）

發表於 更新於
  • 延續上篇的內容，b其實可以水平同時計算

線性代數的角度理解


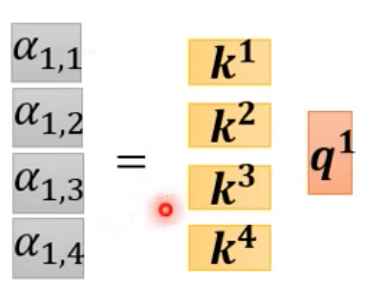
把它延展到$\alpha_{4,4}$

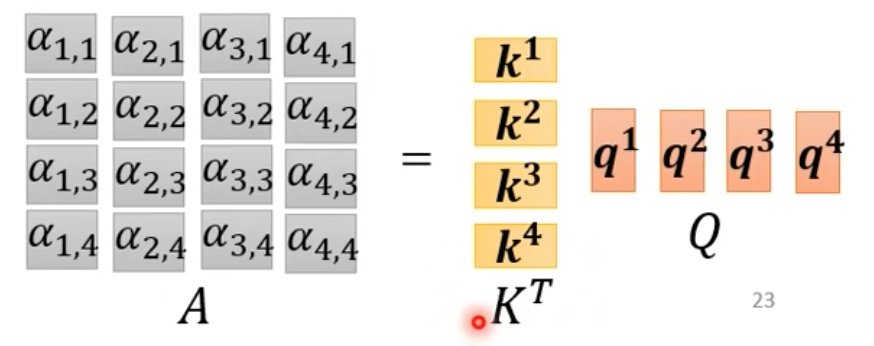
  • 之後再對A做softmax(或其他激發函數)得到A’

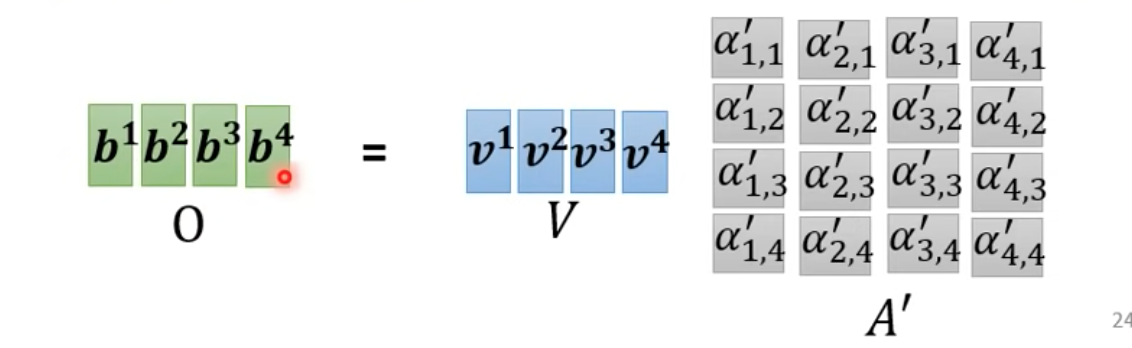
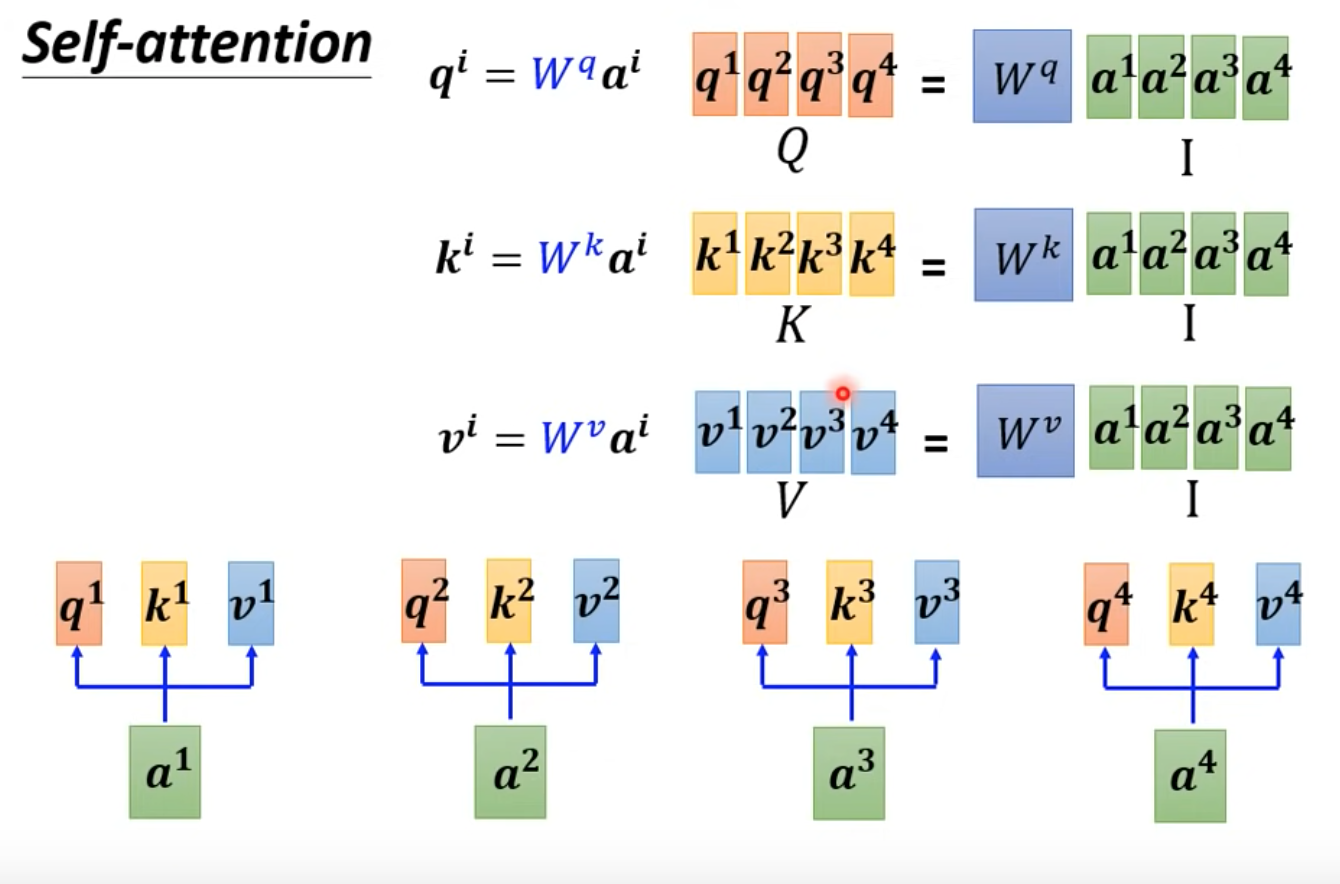
總圖

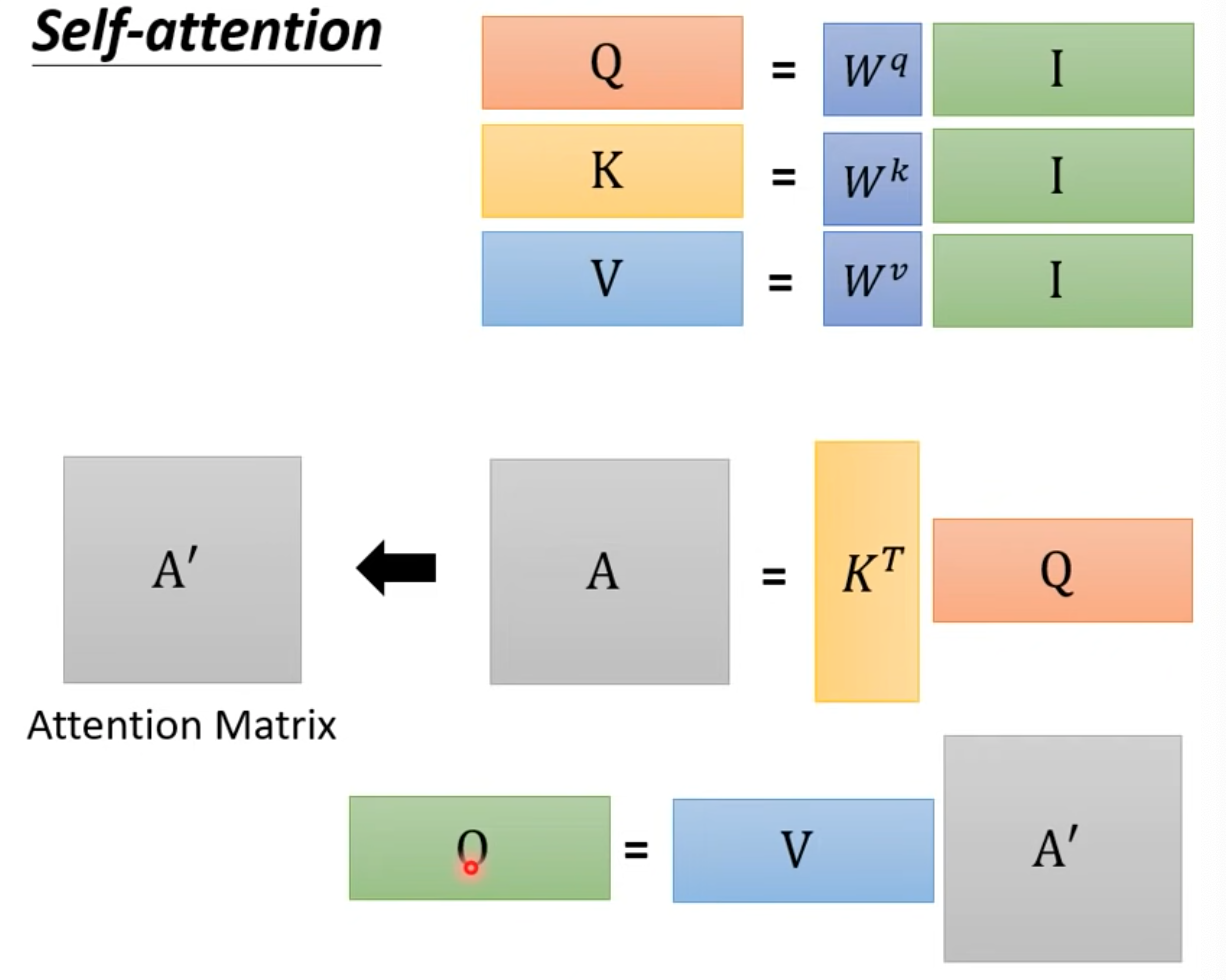
  • 上圖中只有$W^{q,k,v}$training data訓練

Multi-head self-attention

  • 可以把q,k,v產生多個

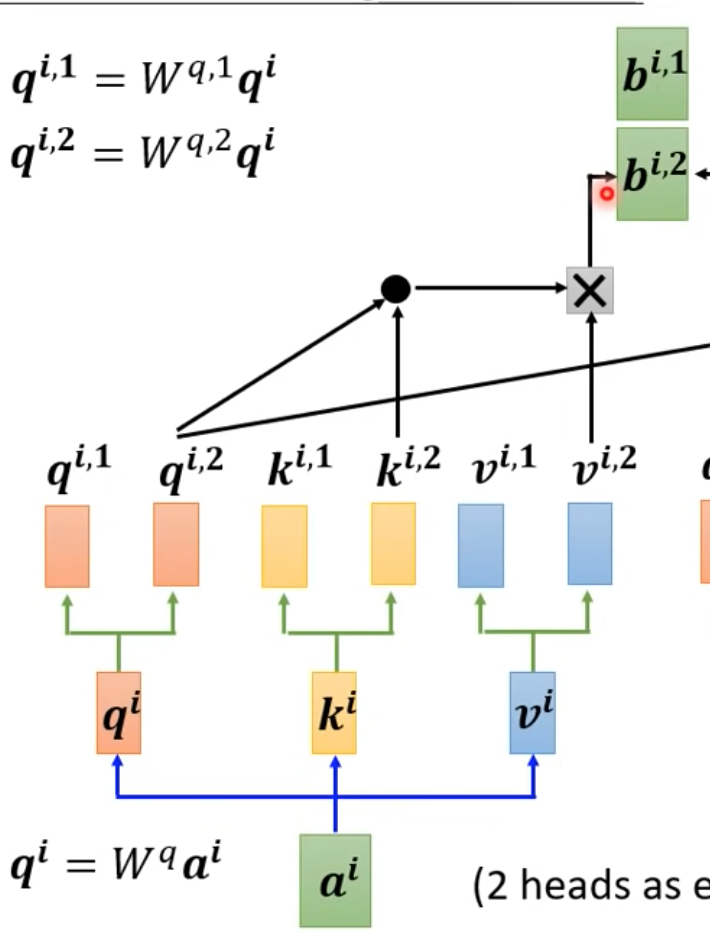
Positional encoding

  • 每一個vector出現在sequence的不同位置可能會有不同的意義
  • 前述之計算並無考慮到相對位置，大家算法都一樣，也都有全部平等的計算
  • 為每一個位置設置一個vector $e^i$，再把這個vector加上$a^i$
  • $e^i$可以透過某個function產生，也可能是hand-crafted
  • 或也可以是learn by data
  • 仍然是尚待研究的主題

Self-attention應用

  • Bert（NLP）
  • transformer

Truncated self-attention

  • 當sequence很大，我們的attention matrix會非常大
  • 一次訓練的時候不要看所有sequence，看某一段就好

Self-attention for image

  • 相片也可以看作是一個vector set，ex. 給定一個5x10 pixel的彩色圖片
    • 把channel當作一個vector(RGB)
    • 則一張圖片是一個5x10的vector set
  • Self-attention GAN
  • DETR

Self-attention v.s CNN

  • CNN會考慮receptive field
  • self-attention則是會考慮整張圖（整個vector set的vector）
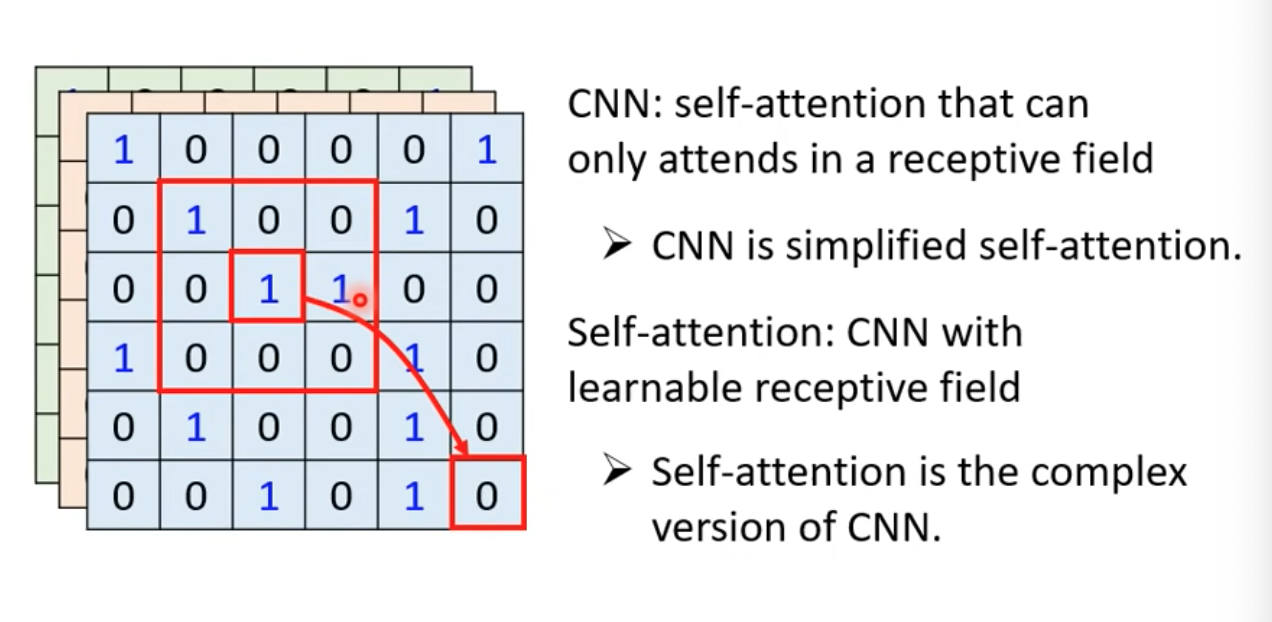
  • self-attention可以說是複雜版、更自由的ＣＮＮ
  • receptive field變成可學習、控制的大小(truncated self attention)
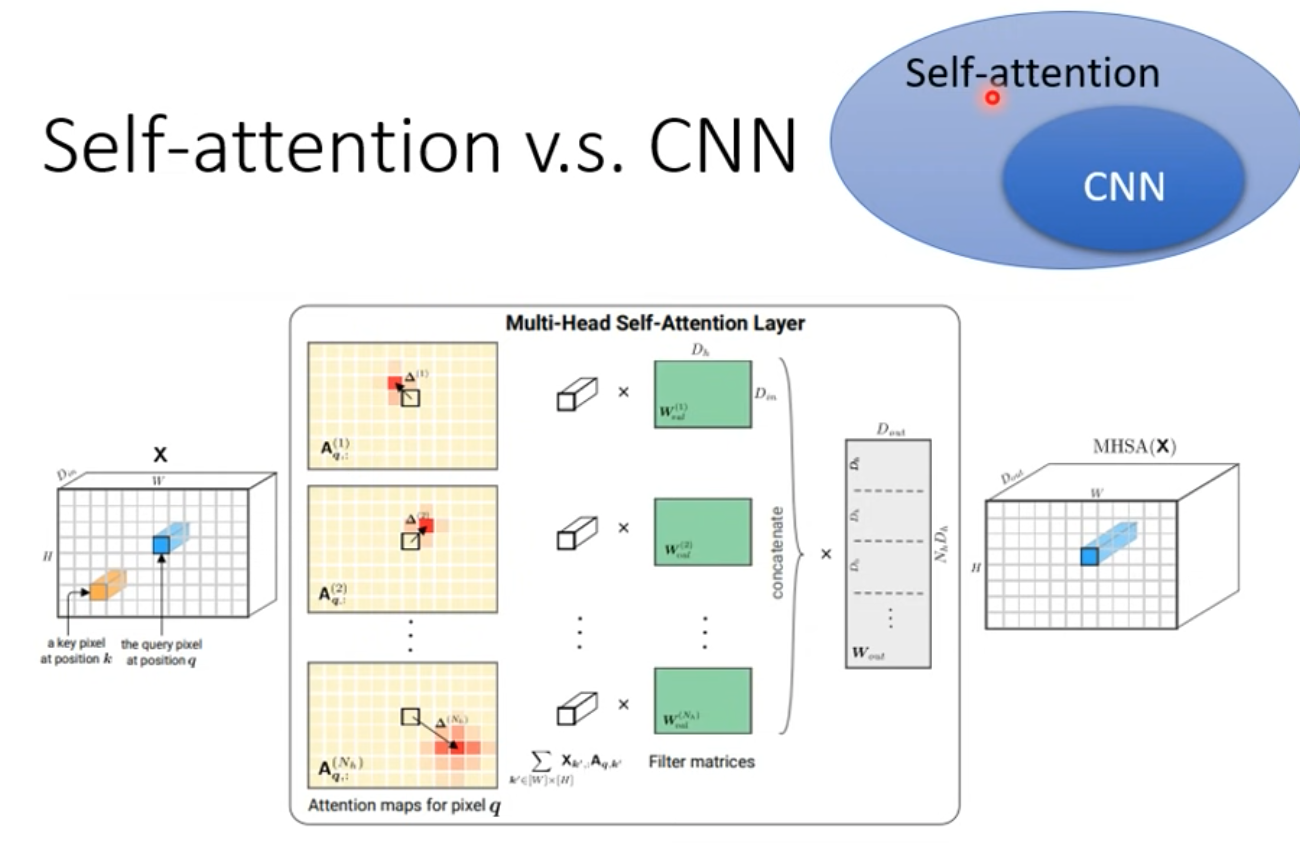
    • Ref. CNN章節
  • 這篇論文用嚴謹的數學證明CNN $\subset$ self-attention
  • Ref.一開始的章節，我們知道更flexible的模型需要更多training data

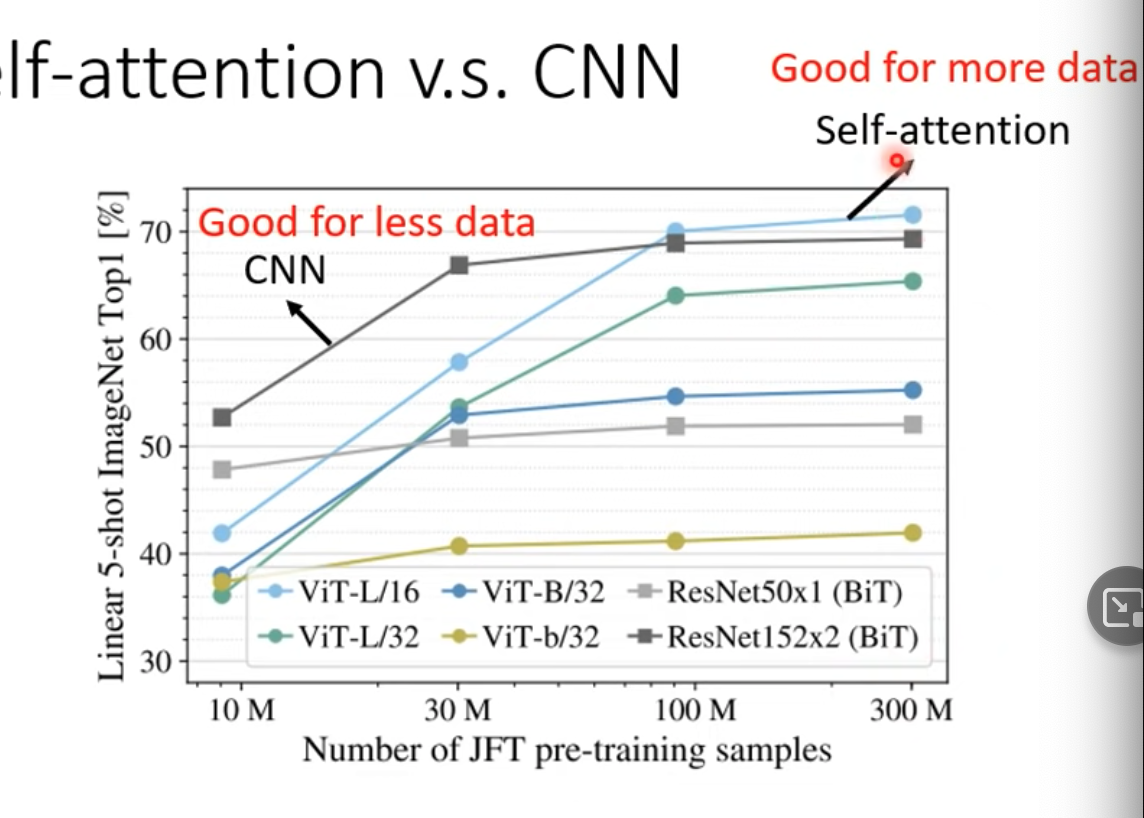
Self-attention v.s RNN

  • RNN不再講到，因為self-attention大多可取代
  • RNN也是處理input是sequence的情況
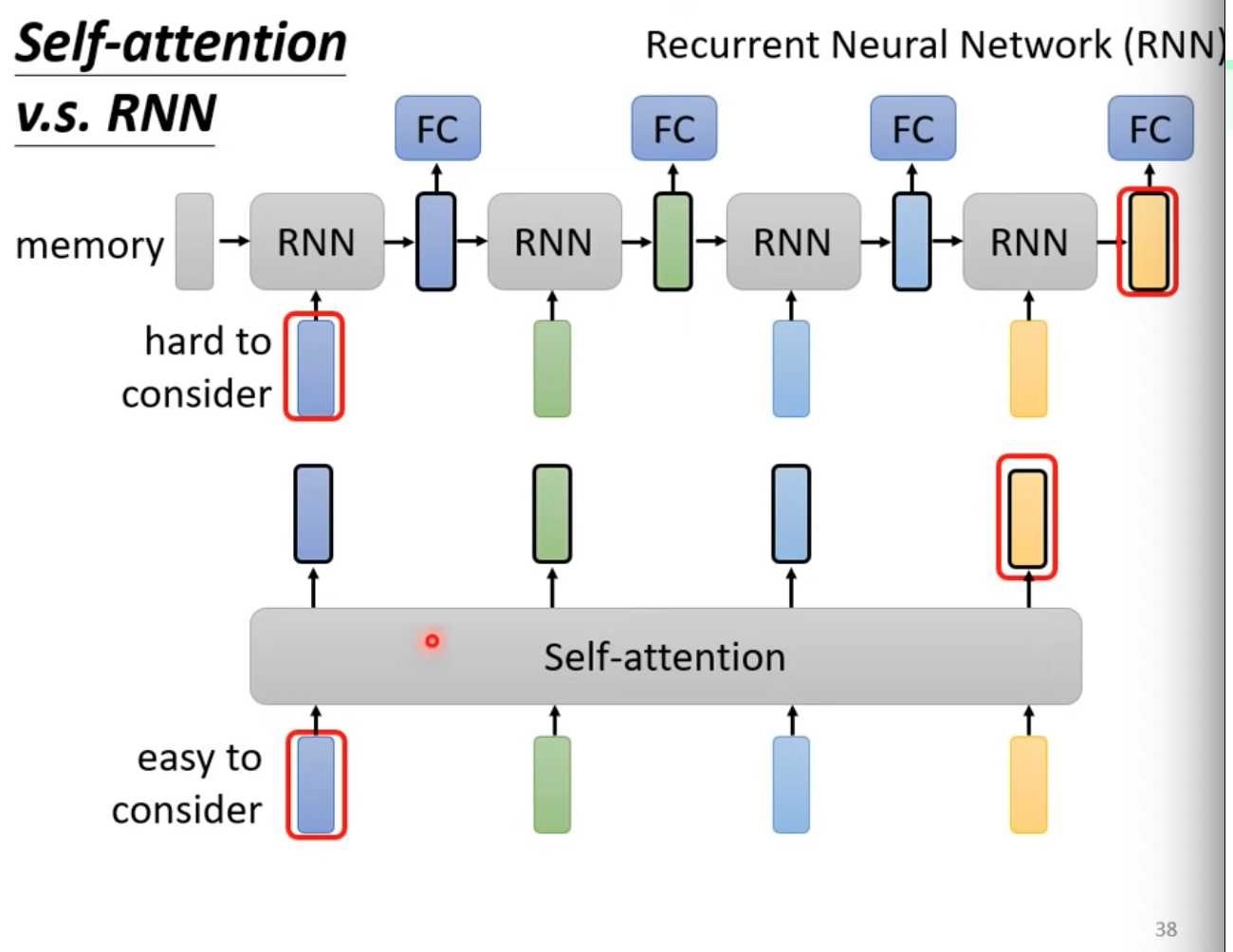
    • 第一個vector做RNN，輸出丟FC，產生輸出，也加入第二個vector丟入RNN…
  • RNN不可以平行處理，self-attention可以
  • RNN難以考慮全面（左右更好），self-attention則可以（天涯若壁鄰）
  • Self-attention加上一些東西以後，其實也能變成RNN(ref.)

Self-attention for graph

  • 因為edge，所以我們知道哪兩個節點之間會有關聯性
  • Attention matrix可以只計算有相連的部分就好
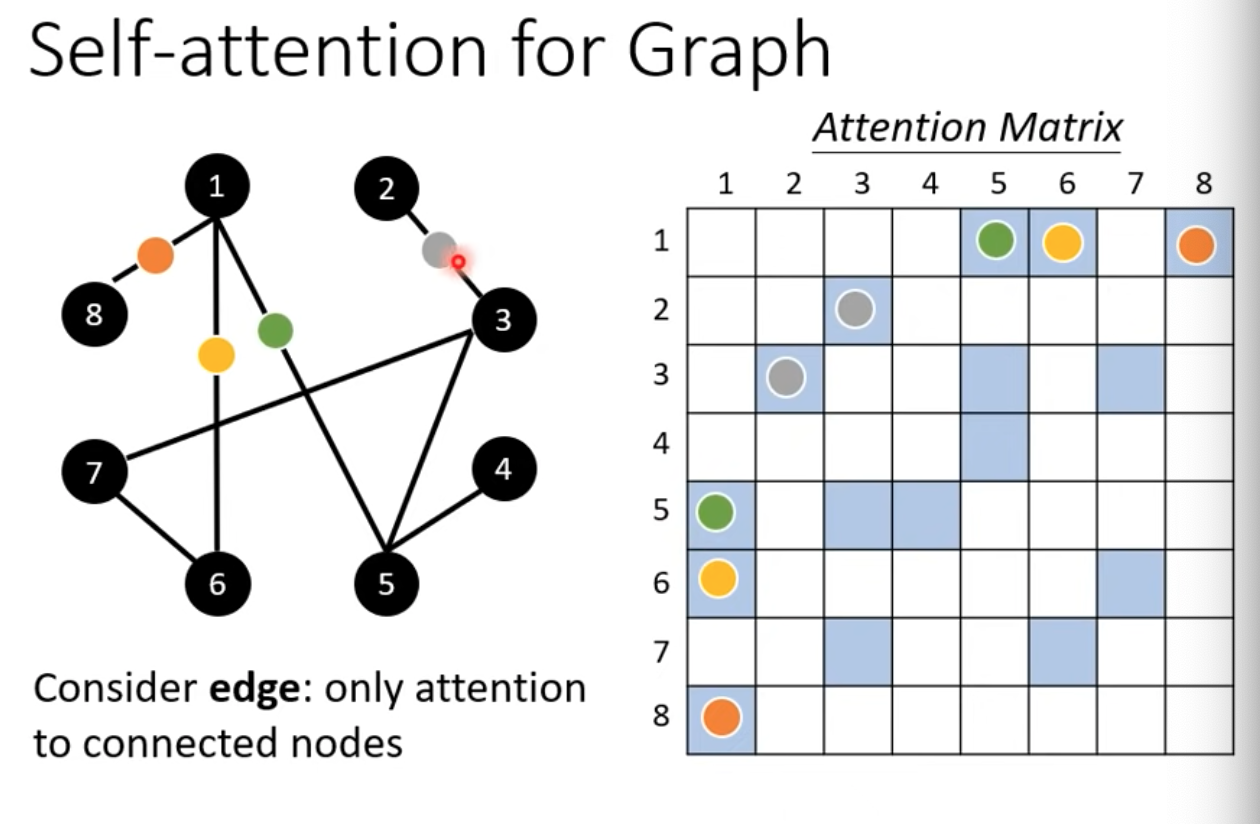
  • 這算是一種Graph neural network (GNN)

GNN REF.

影片1

影片2

結論

  • Self-attention有很多種變形
  • 他的缺點是計算量過大(廣義版CNN…汗)
  • self-attention最早用於transformer
    • 有時候叫transformer其實就是指self-attention
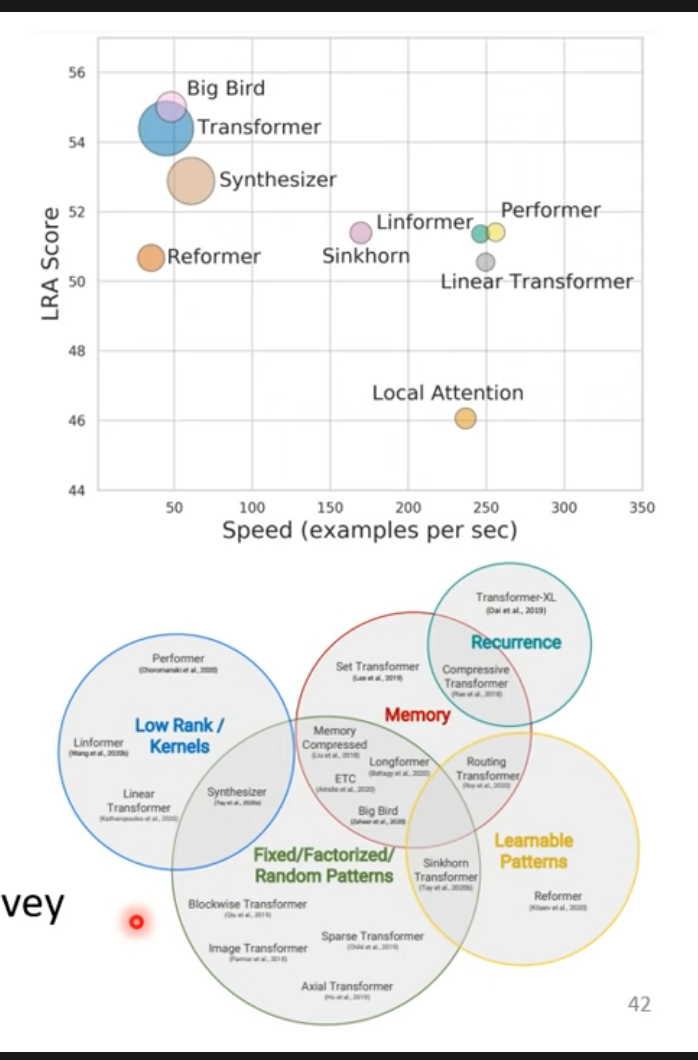
  • performance跟speed的平衡
  • 介紹各式各樣的transformers的變形：Efficient Transformers: A survey