ML_2021_6-2 生成式對抗網路(二) - 理論介紹與WGAN

發表於 更新於

訓練的目標

  • 訓練到底要min/max甚麼東西呢?

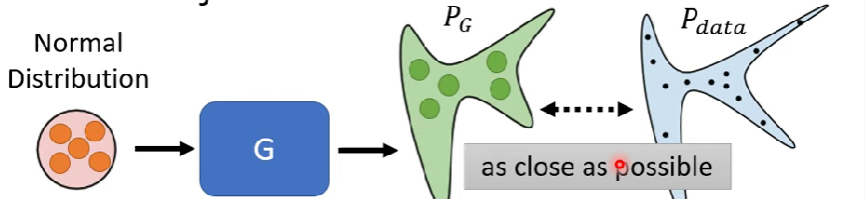
一維的範例

  • 要找的最佳化G參數就是
    $$
    G^* = arg\ min_GDiv(P_G,P_{data})
    $$

  • 其中Div()表示兩個distribution之間的距離(相似度)公式

  • 問題在不知道怎麼計算divergence

  • GAN可以在只有Sample的情況下，估計出div()是多少

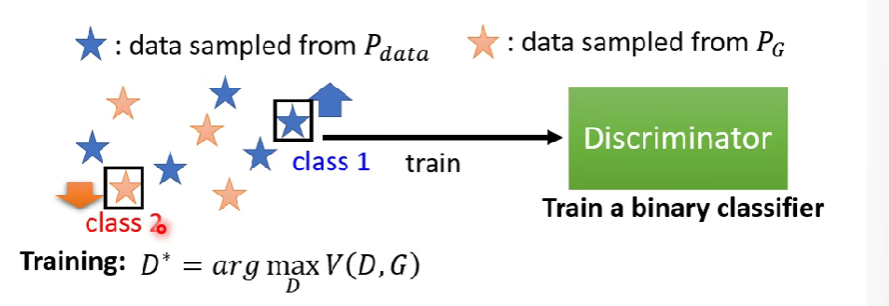
    • 需要從$P_G、P_{data}$取樣，$P_{data}$取自圖庫，而$P_G$則取自generator產生的圖片
         - 這部分就要交給Discriminator，他要max一個objective function，公式有很多種

JS divergence

公式如下(我們要取Max)
   $$
V(G,D) = E_{y\ from\ P_{data}}[logD(y)] + E_{y\ from\ P_G}[log(1-D(y)]
   $$

  • 我們會需要來自data的D(y)越大越好，來自G的D(y)越小越好

Note: 若加上一點自由度，簡化上述公式，可以得到
$$
J^D = -D(x) + D(G(z)), for\ all\ D(x),\ D(G(z))\ \in \ [0,1]
$$
且生成器的損失函數：
$$
J^G = -J^D
$$
因為他們之間彼此對抗，所以他們兩者之間的損失只差一個負號，稱為min-max GAN

  • 其實 $D^*$ 等同於(-1) x cross entropy
    • 早年這麼設計的理由是因為，希望objective function可以跟二元分類扯上關係

  • 參考

  • small divergence，data跟G的圖很像，則hard to discrininate，則small max V(D,G)

  • 因為$max_D\ V(D,G)$與JS divergence有關聯，所以我們可以把Div()換掉，變成
    $$
    G^* = arg\ min_G [max_DV(G,D)] \\\
    D^* = arg\ max_DV(D,G)
    $$
    //D的max objetive value跟JS divergence有關

其他的divergence

  • 當然，我們也可以用不同的divergence

訓練GAN的小技巧

JS divergence 的問題

  • $P_G、P_{data}$重疊的地方往往很少

    • pf1. 圖片是高維空間裡面，低維的manifold
        - 就像在一個平面空間中的兩條線一樣，重合的地方很少
          - 在高維空間內隨便sample的點都不會是圖片
          - 所以他們相交的部分幾乎可以忽略
    • pf2.若$P_G、P_{data}$sample的點不夠多，很容易劃出一個界線把他們切開
      -> $P_G、P_{data}$重疊範圍非常少

  • 若兩個分布沒有重疊的地方，算出來的Div就會永遠都是log 2，看不出差距

WGAN

  • 換一個衡量divergense來衡量2 distribution之相似度

Wasserstein distance

  • 假設一個distribution P為一坨土，而另一個distribution Q為目的地

  • 把土堆P挪到Q所需要的移動距離平均就是Wasserstein distance

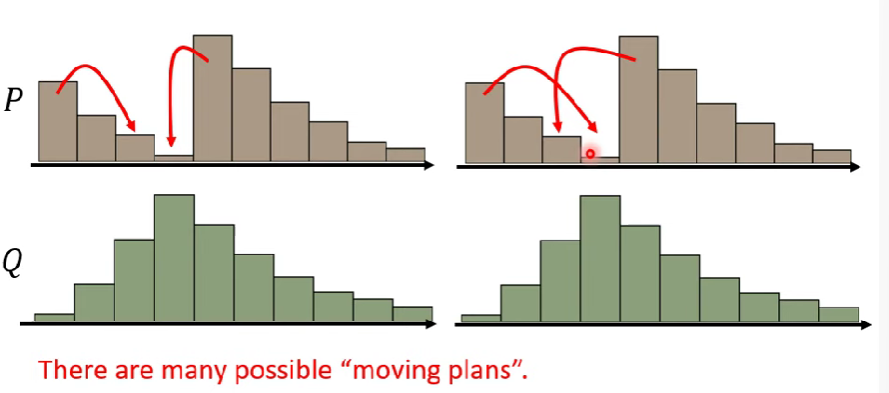
  • 因為可能的挪法很多，所以d會有不同

    • 定義: 窮舉所有的moving plan，找出最小的移動距離當作wasserstein distance
      • 計算麻煩

  • 假設我們能計算Wasserstein distance，帶來的優點:

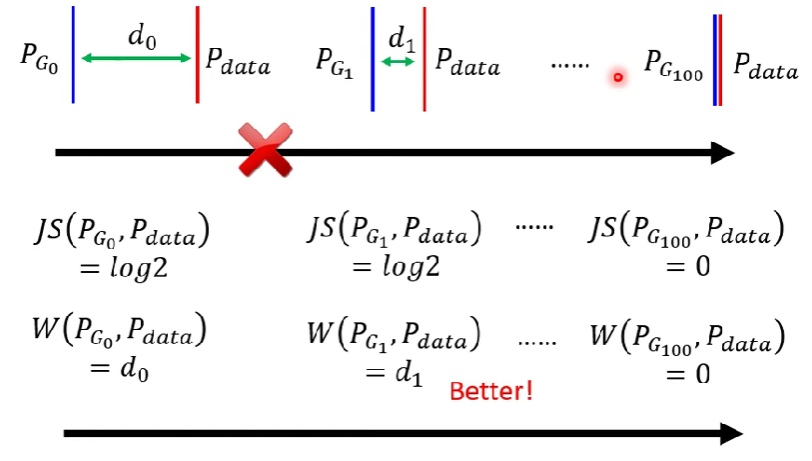
    • 就可以解決JS divergence看不出上圖的好壞比較的問題  

Evaluate Wasserstein distance

  • 解下面的Optimization問題(下圖)，解出來就會是Wasserstein distance

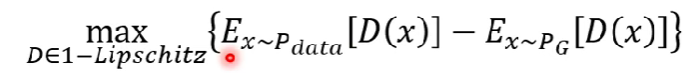
    [、]是期望值，D(x)就是剛剛的D(y)
  • D必須是1-Lipschitz function (Discriminator不可變化劇烈)
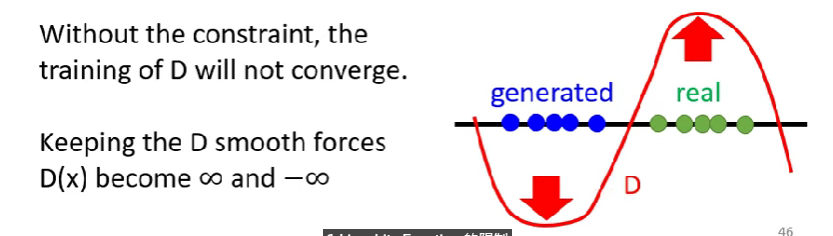
    • 如果沒有這個constraint，則D的training不會收斂
         - 讓D保持smooth強迫D(x)變成無窮與負無窮
    • 基本上就是保證real跟generated的data距離不會太遠

how to 確保這個式子可用

  • 原始GAN方法

    • 強迫network的parameters w bound在[c,-c]
         - 在梯度下降的para更新後，若w>c , w=c ; if w<-c , w = -c
         - 可能可以讓function平滑一點，但沒有解決問題

  • 有一篇 paper : improved WGAN 做的處理方法:

    • 在real data取sample，在fake data取一個sample，在中間再取一個sample，這個sample的梯度需要接近1 (?)

     

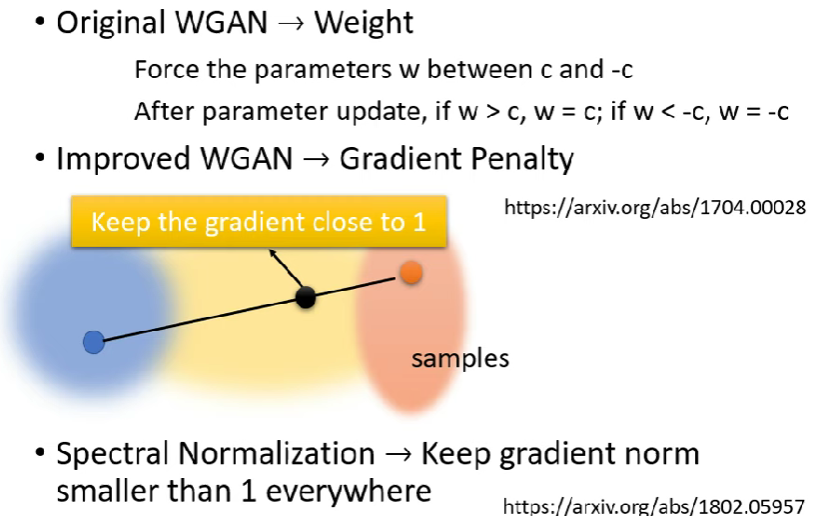
  • 相關方法很多，可以多查查

Q & A

Q1: 在discriminator訓練時，可否加入GAN以往的輸出

A1: 可。實務上跑的時候不會真的讓discriminator被maximize，太花時間，所以通常幾個iteration後就會轉換到generator