ML_2021_10-1 基本概念

發表於

光是正確率高還不夠，若想要讓model放在真實世界運用，還要能防止針對模型的惡意攻擊

  • 本課一樣是舉圖形分類問題為例

How to attack

我們將原本正常的圖片(Benign image)vector都加上一些小小的值，做成Attacked image，則雖然肉眼看不出來，對機器來說卻很容易造成誤判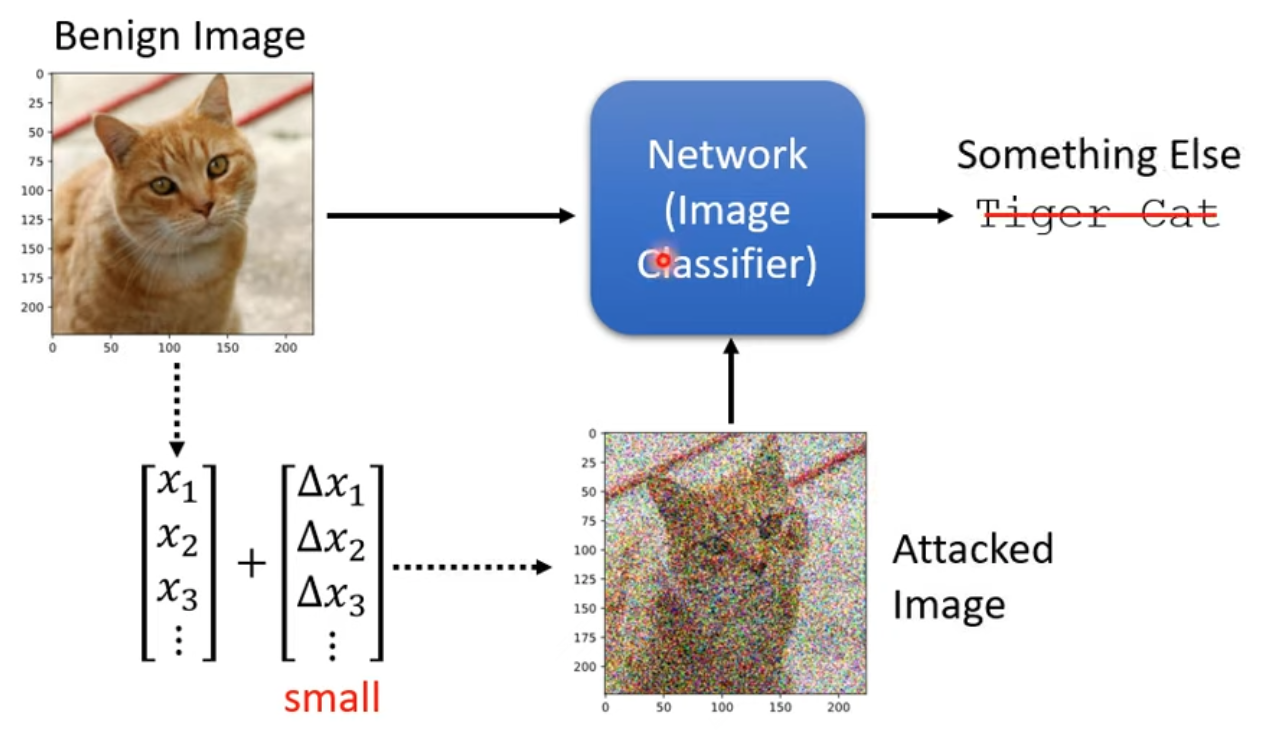
上圖是雜訊被過度加大的結果，正常是什麼都看不出來的

如何找出攻擊的參數

雜訊並非亂加就好，需要解出一個optimization問題
假設原始圖片benign image是$x^0$，則輸出$y^0 = f(x^0)$是一個分布

現在我們想要找到attacked image $\ x^*$，使得他

  1. 與原始$y^0$所屬的類別$\hat{y}$差距越大越好
  2. 與想被誤判的目標類別$y^{target}$越小越好
  3. 與原始圖片$x^0$的差距越小越好（才不會被抓到偷改）

則我們會需要解出一個最佳化圖片$x^*$使
$$
x^* = arg\ min_{d(x^0,x)\leq \epsilon}\ L(x) \\\
L(x) = -e(y,\hat{y}) + e(y,y^{target})
$$
其中e表示cross entropy，L表示loss function，$\epsilon$表示與原圖差距的極限值

原圖與攻擊圖的差距計算

  • 方便計算，這裡均假設他們是一個vector，則原圖與修改圖之間的差距就是他們的向量相減。

    • 問題是，如何定義這樣的差值的距離？

  • 可以用L2-norm或L-infinity等等算法算距離
    差值計算方法與L2、L-infinity的公式

要用哪種norm好呢？
舉例，給定一個圖片，進行兩種修改：
右上角的圖片4個色塊都小量更改; 右下圖片只修改一個色塊但修改較多

則如果套用L2-norm，則兩種改法的距離差一樣，但是如果套用L-infinity，右下的距離會大幅大於右上

為了要瞞過人眼，應該是要讓每張圖的pixel都不會看起來變異過多，故此時應該採用L-infinity更符合實際需求。

Attack approach

要求出$x^*$的步驟

  1. 首先，init parameters，可以直接從$x^0$開始
  2. For t=1 to T，做gradient descend，同訓練模型，此時暫時不考慮上面提到的constraints
    $$
    x^t \leftarrow x^{t-w}-\eta g
    $$

g的算法

  1. 套回剛剛的限制：確認$x^*$與$x^0$差距小於$\epsilon$
    $$
    if\ d(x^0,x^t)> \epsilon: \\\
    \ \ \ x^t \leftarrow fix(x^t)
    $$

現今有很多種的attack method，但精神都不脫離現在的範例，不同的地方主要是

  • optimization的方法
  • Constraints的設計不同

Fast Gradient Sign Method(FGSM)

  • 相關論文

  • 只更新一次參數

  • g裡面的元素只可能是+1,-1

    • 一樣做偏微分，但如果結果為正，輸出1，反之輸出-1

  • 根據$\epsilon$的不同，$x^1 = x^0 - \epsilon g$

  • 這麼做可以確保修正後的圖片可以達到限制的$\epsilon$極值的一個角落

  • 可以嘗試多跑幾個iteration，但這樣有可能就不小心出界了，還需要套用剛剛的constraint，把出界的x拉回來