ML_2021_2-5 類神經網路訓練不起來怎麼辦(四)
Classification as Regression?
Regression長這樣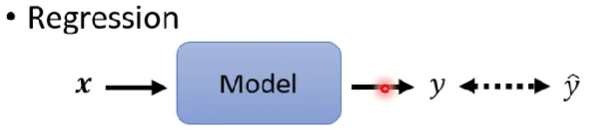
- 那classification怎麼看得像regression呢?
- 我們讓輸出的y(原本是一種類別)變成編號,跟$\hat{y}$比對
- 但這樣會有問題,class 1 跟 class 2 也不同類(loss = 1),但他們的loss會小於class 1 跟 class 3的錯誤預測(loss = 2)
- 常見的做法是把class用one-hot vector來表示
- 當然,這樣我們就會希望output的y是一個向量而非純量 $\rightarrow$ 我們可以用多組的weight去做多次輸出,如下圖
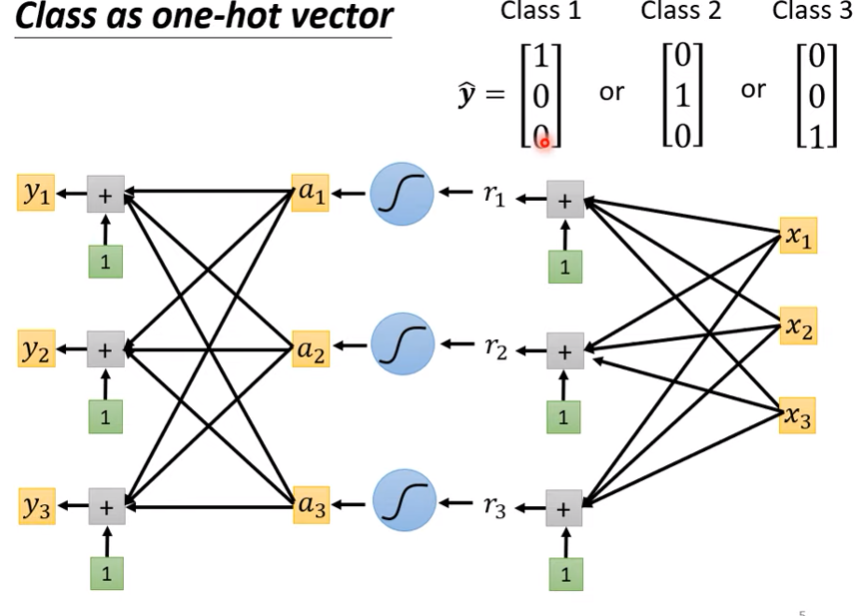
- 我們通常會算出一個y以後,先做一個softmax(y)得到y’才去比較
Softmax activate function
公式如下
$$
y_i’ = \frac{exp(y_i)}{\sum_{j}exp(y_i)}
$$
圖例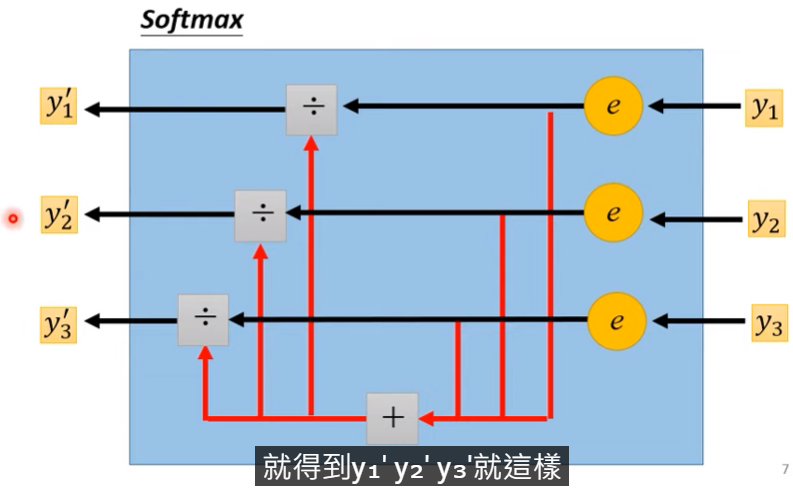
softmax有兩個特徵:
$$
1>y_i>0 \\\
\sum_iy_i’ = 1
$$
- 其實就是把$y_i$的各自機率算出來,若y<0則機率~0
why add softmax at last layer in classification?
- 可以參考原版錄影,因為解釋較長
- 騙小孩的說法是,因為機率是0到1之間,所以我們可以把y做softmax讓他normalize
Note :
- Sigmoid就是2 class版的softmax(Ref.深度學習的數學地圖)
分類模型的loss function
- 我們仍然可以採用MSE來計算
- 但更常用的作法是用cross entropy
cross entropy loss function
公式如下
$$
e = - \sum_i\hat{y}_ilny_i’
$$
- 最小值就是當$y = \hat{y}$
- minimize cross entropy = maximize likelihood
- 基本上softmax是被跟cross entropy綁在一起的,因為向性很高
- 所以如果用cross entropy當loss,那模型最後一層自動就會補上softmax當激發函數(pytorch)
用optimizer的角度來證實cross entropy優於MSE
- 用數學證明的方式說明請參考過去影片
- 以下用舉例的方式說明
- 已知一個模型如下圖

則MSE跟cross entropy的表現如下
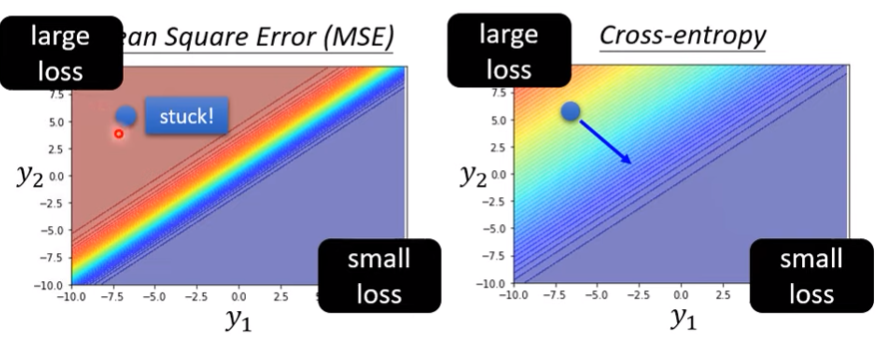
用MSE的前提下,因為點就卡在高loss了,周圍很平坦,很難用梯度下降找到更好的點
這是一個透過改變loss function來改變整個error surface的例子
loss function的定義是有可能影響訓練難度的