ML_2021_3-1 卷積神經網路
- network架構的其中一種變形:CNN
- 此講專注在CNN專門用在影像上的講解(目前也普遍用在影像)
Image classification - Version 1
- 我們需要假設圖片輸入的大小都是固定的
- 如果大小不一,就得要rescale
- 是classification問題,所以輸出one-hot vector (向量的長度代表你能分出多少種類別)
如何把影像當作輸入
- 一張圖片其實是一個3維的Tensor (RGB)
- Tensor(長跟寬),並有3個Channel
- 我們把3維的Tensor拉直,成為一個向量 (這也是為何影像大小需要相同)
Train with fully connected network?
- 如果我們依然使用fully connected network來訓練,又假設neuron取1000個,則一個100x100的圖片輸入,會產生$1001003(彩色)1000 = 310^7$個weight,是一個巨大的數字,大幅增加了overfitting的風險 (彈性過大)
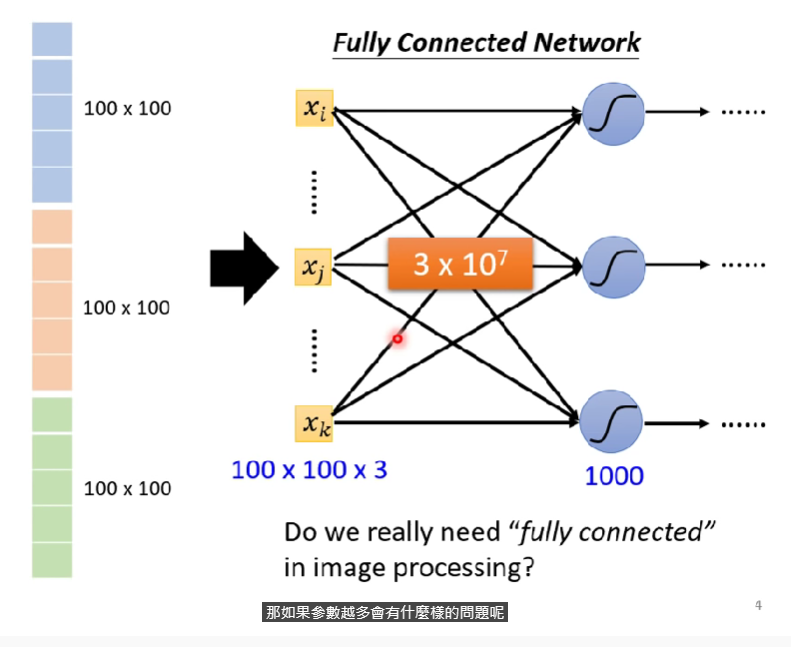
- 不採用全連接層,以下透過一些觀察來嘗試簡化這個網路
Observation 1
- 對於圖片辨識,我們要做的是針對圖片裡面找到一些關鍵的部位 (ex. 鳥嘴、眼睛、翅膀)
- 每個neuron並不需要看過整張圖片(即,不用fully connected)
- 我們可以讓每個neuron只看特定的區塊就好
Simplification 1 - typical settig
CNN會設定一個『Receptive Field』,每個neuron讀取一個他負責的區塊

Receptive Field可以重疊
Different neuron是可以有不同的receptive field的
上述案例裡面,就是3x3的kernel size
通常會有一排(64、128等)個neuron去守備他
不同的receptive field之間的距離差距稱為『stride』
通常receptive field都會高度重疊
如果一個receptive field關注的範圍超出圖片範圍,就需要把外面的值補值(補0、補平均等),稱為『padding』
Receptive fields cover the whole image
Observation 2
- 當一個特殊部位落在不同的receptive field內怎麼處理?
Simplification 2 -typical setting
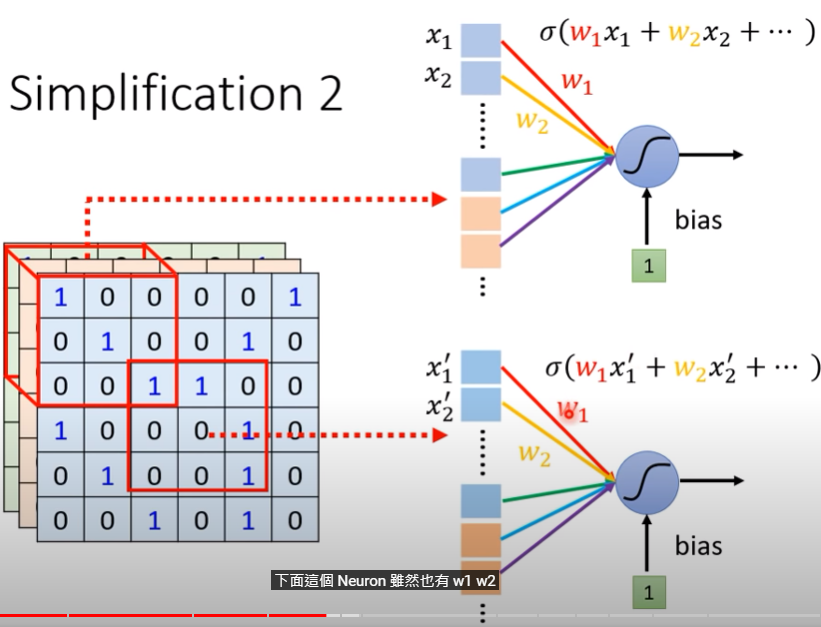
- 我們可以讓一些neuron採用共用參數(Parameter sharing),讓他們的參數都一模一樣
- 因為輸入(receptive field)不一樣,所以各自的輸出也不會相同
- 可能rf1的第一個neuron跟rf2的第一個neuron共用參數,rf1的第二個跟rf2的第二個neuron共參… etc
- 這些共用的參數稱為『Filter』
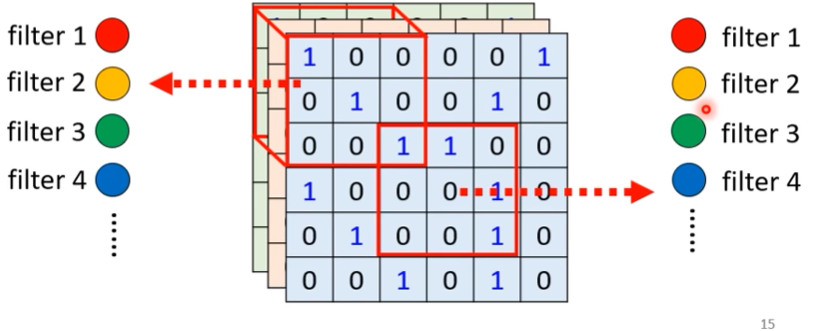
Benefit of Convolutional layer
- 根據上述的觀察,我們成功讓CNN network針對相片輸入的訓練更加簡化
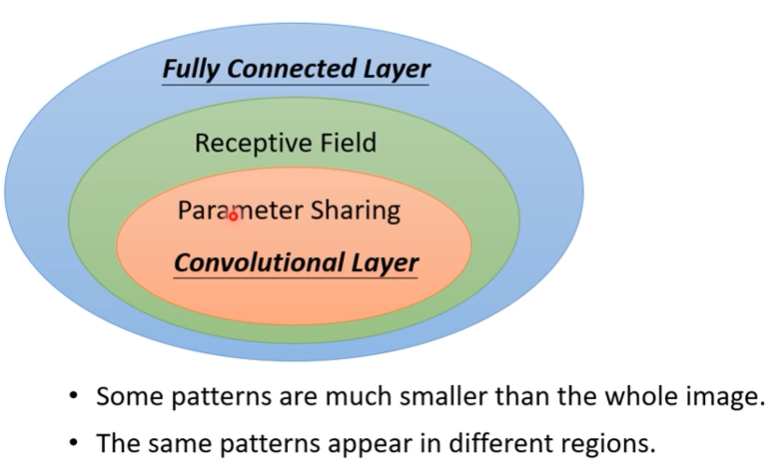
- Convolutional layer的model bias會比較大,但CNN是專門為影像設計的network
PS. 這邊為何CNN bias會比較大,以及為何這樣不好,可以再google一下
另一個說明CNN的版本
Convolutional layer
所謂Convolutional Layer,裡面有很多的Filter,裡面都有一個3x3xchannel維的tensor
每一個filter都是要抓取某個pattern
以下假設是channel = 1(黑白照片)
我們把各個rf跟filter做內積,得出各值
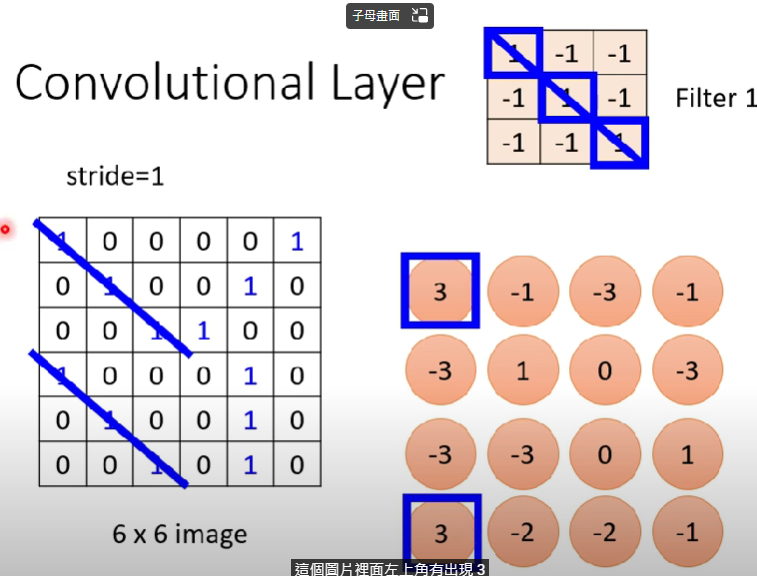
接下來把所有pattern對各filter一樣的計算
這內積出來的一群數字稱為『Feature map』,再這個例子中,我們有64個filter,則我們的feature map會有64組(channels)數字,每組有4x4個數字
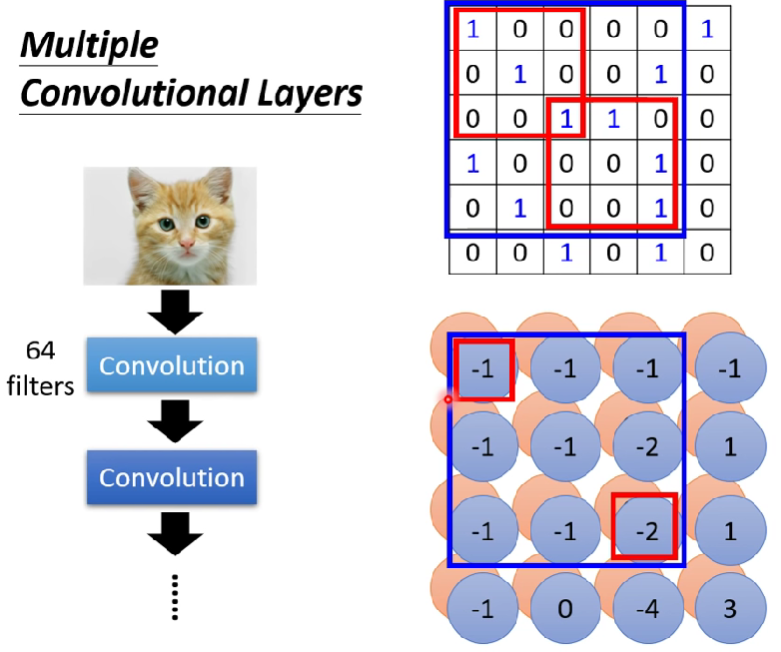
接下來進到第二層的convolution,我們的filter必須變成3x3x64,因為上一層輸出了64個channel,相對於第一層只有一個channel,第二層會出現64個channel
Note:
- 隨著捲積層的深入,我們觀察的圖片pattern會越來越大
- 繼續上面的例子,如果我們的filter之rf一樣是看3x3大小的話,因為我們的feature map中的3x3大小實際上是對應到圖片裡面的5x5大小(跟stride有關),所以其實層數越高,我們一次考慮的範圍會越大!
Comparison of 2 version
- 第一個版本的共用參數,就是第二版本的filter(本slide忽略bias)
- 把一個filter掃過一張圖片,稱作『convolves over』
- 例句(?): each filter convolves over the input image
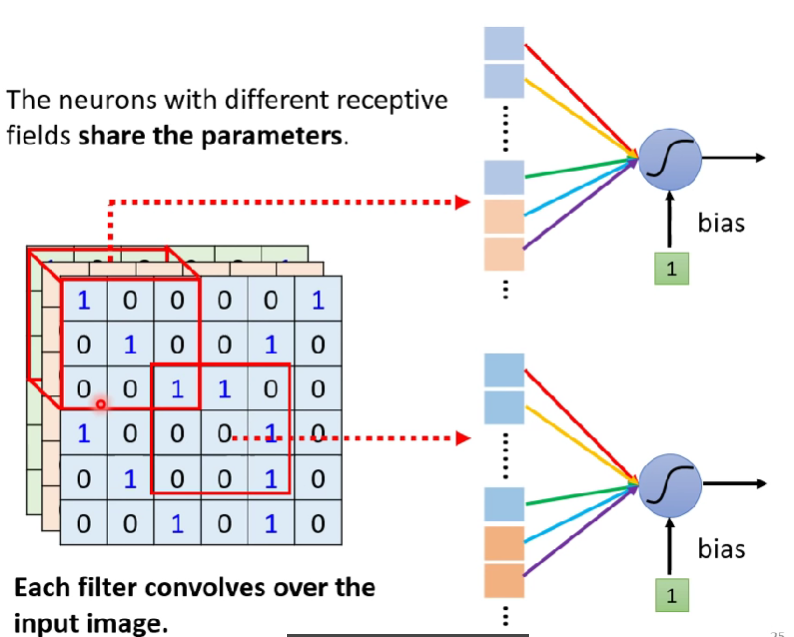
- 例句(?): each filter convolves over the input image

Observation 3
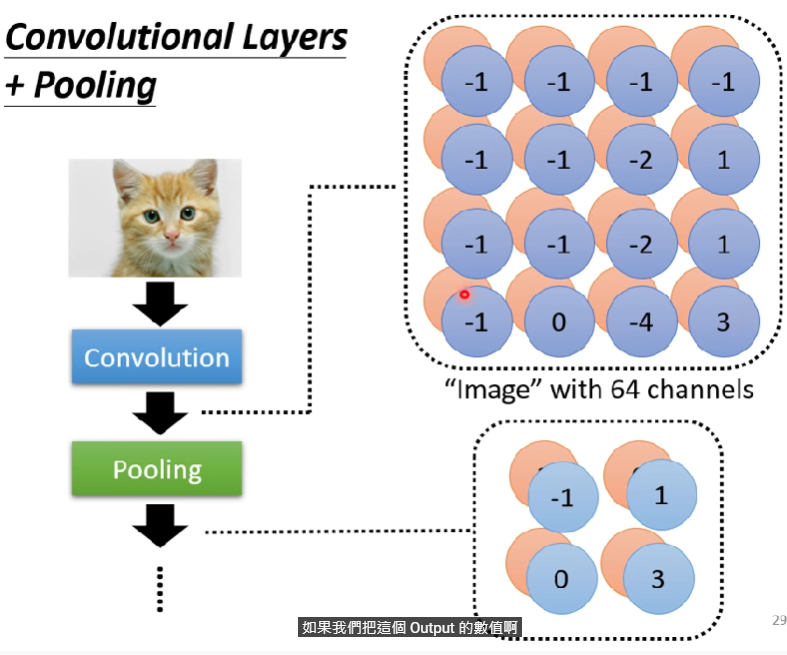
- 如果我們把一張大圖片縮小、拿掉odd columns,圖片還是不會有所影響(看起來差不多),稱為subsampling -> pooling
- Pooling 本身沒有參數,沒有任何東西要learn,有些人稱他為一種激發函數
- pooling就是把圖片像素分組,然後從裡面只選一個像素留下,簡化圖片像素大小
- 下圖為示意圖
- 過度pooling仍會傷害訓練效益
The whole CNN
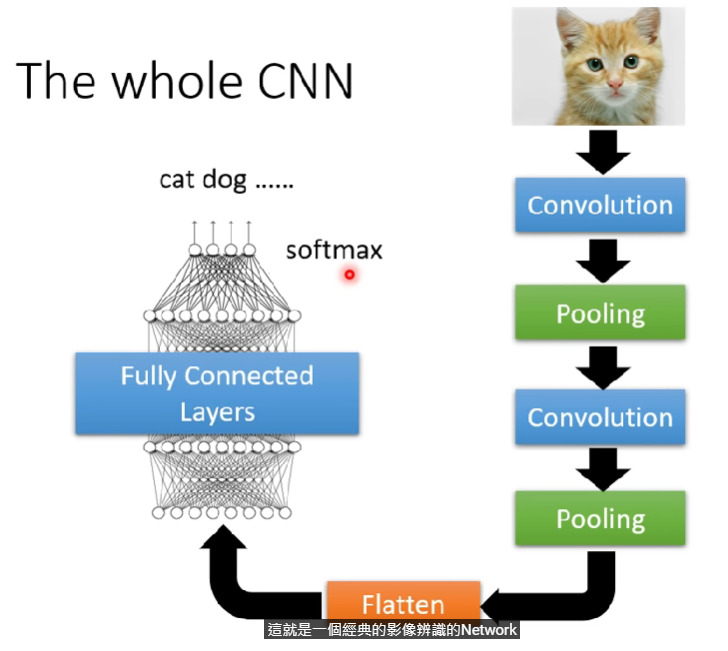
- 做完卷積層以後要做flatten
- flatten就是把矩陣數值拉直
- flatten完以後扔進fully connected layer訓練完,配個softmax(分類),就是一個經典的CNN network
Application: GO
我們用一個19x19的向量來描述一個棋盤,把它扔進network以後輸出next move應該在的位置
下圍棋可以是一個類別分類問題
這個問題也可以用fully-connected network解決
但用CNN效果更好-> 棋盤可以看做一個19x19來描述
每個棋盤格的channel有48個(這格可能被叫吃等等)
這意味著圍棋與影像有許多相似特性
- 可以只看小區塊(alpha go: 5x5)
- Same pattern appear in different regions (雙叫吃等等)
- 可以只看小區塊(alpha go: 5x5)
棋盤可否用pooling ? 因為每格都很重要(精細度高) -> Alpha Go有沒有用呢?
李宏毅教你畫重點XD:學著幫論文畫重點,抓critical terms

alpha go 正文沒有提到神經網路結構,這是在附件找到的
- 視為19x19x48的image
- zero pads(padding補0至23x23)
- 有k個filter(競賽用的go,filter = 192)
- filter的kernel size = 5x5
- stride = 1
- 用到rectifier nonlinearity(ReLU)
- 2~12層都有做zero padding至21x21,filter數同,kernel size = 3x3,stride = 1
- 最後apply softmax function

alpha go 沒有用pooling!!
Hen重要的Notes:
- 語音上、文字處理上,文獻上的方法要仔細看,CNN的receptive field設計會特別為他們特化,這裡講的單純是影像的
- CNN並不能處理影像放大縮小(Scaling)旋轉(Rotation)的問題… (向量問題)
- 為此我們需要data augmentation
- 其實有Network架構(Spatial Transformer Layer)可以解決這個問題,請Ref.這個影片